En este trabajo se describe un modelo numérico para la investigación de los procesos de erosión, transporte y sedimentación a gran escala asociados a la génesis de inundación. El modelo asume que el principal medio de transporte de sedimentos durante la inundación fue haciendo fluir rápidamente el agua turbulenta. El movimiento del agua es impulsada por los tsunamis de gran amplitud que se generan en las zonas de subducción como la placa de subducción y la placa superior, después de haber sido bloqueada durante un intervalo de tiempo, de repente liberación y deslice rápidamente una sobre otra. Mientras que las dos placas adyacentes están bloqueadas, el fondo del mar es arrastrado hacia abajo por la placa litosférica se hunde de forma constante por debajo. Cuando las placas se desbloquean, el fondo del mar se recupera rápidamente, generando un tsunami de gran amplitud. Teoría para el flujo turbulento de canal abierto se aplica al modelo de la suspensión, el transporte, y la deposición de sedimentos. La cavitación se supone que es el mecanismo dominante responsable de la erosión de la roca madre, así como del sedimento ya depositada. El modelo trata el agua en la superficie de la tierra en rotación en términos de una sola capa vertical, pero con altura inferior variable. cálculos ilustrativos muestran que con opciones de parámetros plausibles promedio de las tasas de erosión y sedimentación del orden de 12 m / día (0,5 m / h) se producen, suficiente dentro de un intervalo de 150 días durante la inundación para dar cuenta de los aproximadamente 1800 m (5905 pies) espesor medio de sedimentos fanerozoicas que cubren la superficie continental de la tierra hoy en día. Un notable descubrimiento de estos cálculos es que los tsunamis que inciden sobre las costas continentales producen una viruta de agua sobre el interior de los continentes. Hasta que se alcanza el equilibrio, más agua se realiza sobre la superficie continental por los tsunamis que pueden drenar por gravedad. En los ejemplos ilustrativos, los niveles de agua sostenidos por encima del continente en lugares elevan a más de un kilómetro por encima del nivel del mar originales. Tal aguas profundas sobre el continente permite grandes espesores de sedimentos se acumulen en la parte superior de la superficie del continente por encima del nivel medio del mar global. Aunque la más intensa erosión del lecho de roca continental se produce a lo largo del margen continental, porciones significativas del interior del continente también sufren una erosión significativa, plausiblemente representando escudos continentales de hoy en día.
Palabras clave: Génesis Inundación, catastróficos tectónica global placa, tsunamis gigantes, transporte de sedimentos, erosión de cavitación turbulenta, flujo de canal abierto, de aproximación aguas poco profundas
Palabras clave: Génesis Inundación, catastróficos tectónica global placa, tsunamis gigantes, transporte de sedimentos, erosión de cavitación turbulenta, flujo de canal abierto, de aproximación aguas poco profundas
Introducción
La contabilización de las secuencias de sedimentos gruesos que cubren la superficie de los continentes es un tema de suma importancia para la comprensión de los aspectos físicos de la inundación del Génesis. En las regiones de la plataforma continental, como el corazón de los EE.UU., la secuencia de capas de sedimentos que contienen fósiles son comúnmente 2000 m (6561 pies) o más de espesor acumulado (Prothero y Schwab 2004, 12-14). También suelen mostrar una continuidad asombrosa horizontal (por ejemplo, Ager 1973). Qué clase de procesos físicos podría haber movido tan grandes volúmenes de sedimentos y dispuestas en dichas lateralmente extensas capas ordenadas, dentro del lapso de un año, ya que requiere la Escritura? Como un ejercicio preliminar se puede hacer estimaciones aproximadas de las tasas de erosión, transporte de sedimentos, y de deposición que se necesitan. Si asumimos que la mayor parte de la deposición primaria se produjo dentro del intervalo de 150 días durante el cual "el agua que prevalecía en la tierra" (Génesis 7:24), podemos calcular una tasa promedio deposición durante ese intervalo necesario para producir una columna de sedimentos , digamos, 1800 m (5905 pies) de espesor, que es el valor medio durante los continentes de hoy. Dividiendo 1800 m (5905 pies) por 150 días produce una tasa promediada en el tiempo de deposición de 12 m / día (0,5 m / h o 1,4 × 10 -4 m / s). También sugiere una velocidad promediada en el tiempo comparable de la erosión.
La gran extensión lateral de la mayoría de las capas sugiere distancias de transporte significativos. Supongamos que la distancia media entre los sitios de la erosión y la deposición es de 1000 km (621 mi) (1 × 10 6 m) y que la velocidad media del agua es de 20 m / s (45 mph). Una partícula típica de sedimentos en suspensión es, por tanto, para (1 × 10 6m) / (20 m / s) = 5 × 10 4 s (13,9 h). Si la entrada y salida de la tubería, por así decirlo, es la velocidad de erosión / deposición de 1,4 × 10 -4 m / s, a continuación, la carga media en suspensión de sedimentos distribuido verticalmente a través de la lámina de agua que fluye debe ser (1,4 × 10 - 4 m / s) x (5 × 10 4 s) = 7 m. Esto requiere que la profundidad del agua que fluye sea lo suficientemente grande y también su turbulencia suficientemente intenso como para mantener este tipo de carga suspendida. A partir de estos cálculos simples, es obvio que cualquier mecanismo candidato viable implica probablemente hojas coherentes de agua turbulenta al menos muchas decenas de metros de profundidad panorámicas sobre la superficie de la tierra a velocidades de al menos varias decenas de m / s. Dado que se trata de estimaciones promediadas en el tiempo, cuando se toma la probabilidad de variación de tiempo significativo, incluso episodicity, en cuenta, las profundidades de agua y velocidades pico deben haber sido mucho mayor.
Lo que el agua podría haber causado a moverse con tal vigor través de las superficies continente? El mecanismo asumido en este trabajo es una consecuencia lógica de la gran cantidad de subducción de la litosfera oceánica que se produjo durante el diluvio del Génesis (Baumgardner 2003). En el mundo actual, la subducción de placas y primordiales están bloqueados a lo largo de la mayor parte de más de 65.000 kilometros de la Tierra (40.389 millas) de las zonas de subducción. El movimiento de una placa en subducción en relación con la losa adyacente primordial ocurre típicamente en sacudidas repentinas, o eventos de ruptura. La ruptura se produce cuando la tensión alcanza un nivel en el que las asperezas de bloqueo de las dos placas a lo largo de las vacaciones de superficie de la falla, lo que resulta en un movimiento repentino largo de la falla y la liberación de energía sísmica o un terremoto considerable.Parece probable que este mismo proceso de bloqueo y ruptura repentina también ocurrieron durante la inundación, excepto con mucha más frecuencia. Para una velocidad de la placa de 2 m / s (6,5 pies / s) y un ángulo de subducción de 45 °, sólo alrededor de una hora se necesita para tirar hacia abajo la placa superior de 5000 m (16.404 pies).repentina ruptura de dicha zona bloqueada genera un terremoto y el tsunami resultante con gran amplitud, más grande que cualquier testigo en la historia registrada desde el diluvio. En nuestros cálculos ilustrativos suponemos arbitrariamente 16 zonas de subducción, cada 2000 km (1.242 millas) de longitud, que abren sucesivamente después de haber sido bloqueada durante aproximadamente una hora a la correa un tsunami gigante en algún lugar del océano global cada cuatro minutos. Los cálculos numéricos muestran que tales forzando es más que suficiente para alcanzar y mantener la velocidad del agua requeridos. Para fallos cerradas que se deslizan y rebote con 5000 m (16.404 pies), la velocidad del agua picos alcanzan cerca de 200 m / s, y velocidades medias de columna de agua alcanzan valores de muchas decenas de m / s. La turbulencia es lo suficientemente fuerte para mantener muchas decenas de metros de sedimentos en suspensión como barridos de agua a través de la superficie continental. La turbulencia es el mecanismo físico que permite y mantiene tan alto volumen y el transporte de larga distancia de sedimento.
Este documento es una revisión de un documento (Baumgardner 2013) presenté en la Séptima Conferencia Internacional sobre Creacionismo. La principal diferencia en el artículo anterior y éste es el mecanismo para accionar el movimiento del agua. En el artículo anterior, he invocado por las mareas producidas cerca de los encuentros de un cuerpo de tamaño de una luna con la tierra. En este trabajo los tsunamis generados por el bloqueo y deslizamiento y el rebote de los segmentos de falla a lo largo de las zonas de subducción, un aspecto esperado de las placas tectónicas catastróficas repentina, son el mecanismo principal de conducción de las aguas turbulentas. Los tratamientos numéricos de flujo de agua, la suspensión de sedimentos, la erosión y la deposición de sedimentos, sin embargo, son en gran parte el mismo que el descrito en el documento 2013. Para guardar el lector interesado de este trabajo de necesitar varias veces para referirse al documento anterior para entender los detalles de los tratamientos y métodos que se aplican en este trabajo, he reproducido esos detalles aquí en los Apéndices A-G.
La contabilización de las secuencias de sedimentos gruesos que cubren la superficie de los continentes es un tema de suma importancia para la comprensión de los aspectos físicos de la inundación del Génesis. En las regiones de la plataforma continental, como el corazón de los EE.UU., la secuencia de capas de sedimentos que contienen fósiles son comúnmente 2000 m (6561 pies) o más de espesor acumulado (Prothero y Schwab 2004, 12-14). También suelen mostrar una continuidad asombrosa horizontal (por ejemplo, Ager 1973). Qué clase de procesos físicos podría haber movido tan grandes volúmenes de sedimentos y dispuestas en dichas lateralmente extensas capas ordenadas, dentro del lapso de un año, ya que requiere la Escritura? Como un ejercicio preliminar se puede hacer estimaciones aproximadas de las tasas de erosión, transporte de sedimentos, y de deposición que se necesitan. Si asumimos que la mayor parte de la deposición primaria se produjo dentro del intervalo de 150 días durante el cual "el agua que prevalecía en la tierra" (Génesis 7:24), podemos calcular una tasa promedio deposición durante ese intervalo necesario para producir una columna de sedimentos , digamos, 1800 m (5905 pies) de espesor, que es el valor medio durante los continentes de hoy. Dividiendo 1800 m (5905 pies) por 150 días produce una tasa promediada en el tiempo de deposición de 12 m / día (0,5 m / h o 1,4 × 10 -4 m / s). También sugiere una velocidad promediada en el tiempo comparable de la erosión.
La gran extensión lateral de la mayoría de las capas sugiere distancias de transporte significativos. Supongamos que la distancia media entre los sitios de la erosión y la deposición es de 1000 km (621 mi) (1 × 10 6 m) y que la velocidad media del agua es de 20 m / s (45 mph). Una partícula típica de sedimentos en suspensión es, por tanto, para (1 × 10 6m) / (20 m / s) = 5 × 10 4 s (13,9 h). Si la entrada y salida de la tubería, por así decirlo, es la velocidad de erosión / deposición de 1,4 × 10 -4 m / s, a continuación, la carga media en suspensión de sedimentos distribuido verticalmente a través de la lámina de agua que fluye debe ser (1,4 × 10 - 4 m / s) x (5 × 10 4 s) = 7 m. Esto requiere que la profundidad del agua que fluye sea lo suficientemente grande y también su turbulencia suficientemente intenso como para mantener este tipo de carga suspendida. A partir de estos cálculos simples, es obvio que cualquier mecanismo candidato viable implica probablemente hojas coherentes de agua turbulenta al menos muchas decenas de metros de profundidad panorámicas sobre la superficie de la tierra a velocidades de al menos varias decenas de m / s. Dado que se trata de estimaciones promediadas en el tiempo, cuando se toma la probabilidad de variación de tiempo significativo, incluso episodicity, en cuenta, las profundidades de agua y velocidades pico deben haber sido mucho mayor.
Lo que el agua podría haber causado a moverse con tal vigor través de las superficies continente? El mecanismo asumido en este trabajo es una consecuencia lógica de la gran cantidad de subducción de la litosfera oceánica que se produjo durante el diluvio del Génesis (Baumgardner 2003). En el mundo actual, la subducción de placas y primordiales están bloqueados a lo largo de la mayor parte de más de 65.000 kilometros de la Tierra (40.389 millas) de las zonas de subducción. El movimiento de una placa en subducción en relación con la losa adyacente primordial ocurre típicamente en sacudidas repentinas, o eventos de ruptura. La ruptura se produce cuando la tensión alcanza un nivel en el que las asperezas de bloqueo de las dos placas a lo largo de las vacaciones de superficie de la falla, lo que resulta en un movimiento repentino largo de la falla y la liberación de energía sísmica o un terremoto considerable.Parece probable que este mismo proceso de bloqueo y ruptura repentina también ocurrieron durante la inundación, excepto con mucha más frecuencia. Para una velocidad de la placa de 2 m / s (6,5 pies / s) y un ángulo de subducción de 45 °, sólo alrededor de una hora se necesita para tirar hacia abajo la placa superior de 5000 m (16.404 pies).repentina ruptura de dicha zona bloqueada genera un terremoto y el tsunami resultante con gran amplitud, más grande que cualquier testigo en la historia registrada desde el diluvio. En nuestros cálculos ilustrativos suponemos arbitrariamente 16 zonas de subducción, cada 2000 km (1.242 millas) de longitud, que abren sucesivamente después de haber sido bloqueada durante aproximadamente una hora a la correa un tsunami gigante en algún lugar del océano global cada cuatro minutos. Los cálculos numéricos muestran que tales forzando es más que suficiente para alcanzar y mantener la velocidad del agua requeridos. Para fallos cerradas que se deslizan y rebote con 5000 m (16.404 pies), la velocidad del agua picos alcanzan cerca de 200 m / s, y velocidades medias de columna de agua alcanzan valores de muchas decenas de m / s. La turbulencia es lo suficientemente fuerte para mantener muchas decenas de metros de sedimentos en suspensión como barridos de agua a través de la superficie continental. La turbulencia es el mecanismo físico que permite y mantiene tan alto volumen y el transporte de larga distancia de sedimento.
Este documento es una revisión de un documento (Baumgardner 2013) presenté en la Séptima Conferencia Internacional sobre Creacionismo. La principal diferencia en el artículo anterior y éste es el mecanismo para accionar el movimiento del agua. En el artículo anterior, he invocado por las mareas producidas cerca de los encuentros de un cuerpo de tamaño de una luna con la tierra. En este trabajo los tsunamis generados por el bloqueo y deslizamiento y el rebote de los segmentos de falla a lo largo de las zonas de subducción, un aspecto esperado de las placas tectónicas catastróficas repentina, son el mecanismo principal de conducción de las aguas turbulentas. Los tratamientos numéricos de flujo de agua, la suspensión de sedimentos, la erosión y la deposición de sedimentos, sin embargo, son en gran parte el mismo que el descrito en el documento 2013. Para guardar el lector interesado de este trabajo de necesitar varias veces para referirse al documento anterior para entender los detalles de los tratamientos y métodos que se aplican en este trabajo, he reproducido esos detalles aquí en los Apéndices A-G.
La formulación matemática
El énfasis de este trabajo es el uso de la modelización numérica para explorar la erosión a gran escala, el transporte de sedimentos y procesos de deposición que operaron durante el diluvio del Génesis como se infiere de los sedimentos cubriendo los continentes de hoy. Las características prominentes del registro sedimentario, como se explica en la introducción, sugieren que las láminas de agua turbulenta barriendo sobre la superficie continente deben haber jugado un papel importante. Tal movimiento de agua está en la categoría general de límite turbulenta flujo de la capa, que es de gran interés práctico y uno que se ha estudiado experimentalmente por muchos años. En la comunidad de ingeniería hidrológica, este tipo de flujo de agua se refiere al flujo de canal como abierta. Ejemplos de flujos de canal abierto incluyen los ríos, las corrientes de marea, canales de riego, y láminas de agua corriendo a través de la superficie del suelo después de una lluvia. Las ecuaciones usadas comúnmente para modelar estas corrientes están anclados en las mediciones experimentales y décadas de validación en muchas aplicaciones diversas. Es la turbulencia del agua que fluye en dichos flujos que mantiene las partículas de sedimento en suspensión. El Diario de Ingeniería Hidráulica no es sino una de varias revistas que se ha publicado una gran cantidad de documentos en el flujo de canal abierto turbulento y el transporte de sedimentos en las últimas décadas.
Apéndice A se resumen las observaciones, experimentos, y los esfuerzos para formular una descripción matemática de la turbulencia del fluido en los dos últimos siglos. Una descripción de flujo de fluido turbulento proporcionado hace casi un siglo por el científico británico LF Richardson (1920) sigue siendo válida hoy en día. Su descripción es un flujo cuyos movimientos se caracterizan por una jerarquía de vórtices, o remolinos, de grande a pequeño. Estos remolinos, incluidas las grandes, son inestables. La cizalla que su rotación ejerce sobre el fluido que rodea genera más pequeñas nuevas remolinos. La energía cinética de los remolinos grandes se pasa así a los remolinos más pequeños que surgen de ellos. Estos remolinos más pequeños a su vez se someten a un mismo proceso, dando lugar a remolinos aún más pequeñas que heredan la energía de sus predecesores, y así sucesivamente. De esta manera, la energía se transmite de las grandes escalas de movimiento a escalas más y más pequeños hasta alcanzar una escala de longitud suficientemente pequeño que la viscosidad molecular del fluido transforma la energía cinética de estos remolinos más pequeños en calor.
Cuando un fluido se está moviendo con respecto a una superficie fija, la velocidad del fluido, comenzando desde cero en el límite, los aumentos-primeros rápidamente, y luego menos rápidamente-como la distancia desde la superficie aumenta. La región adyacente a la superficie en la que la velocidad media del flujo paralelo a la superficie aún está cambiando, al menos modestamente, ya que uno se aleja de la superficie es conocida como la capa límite. Cuando la velocidad del fluido sobre la superficie es suficientemente alta, la capa límite se vuelve turbulento y se llena de remolinos que pueden abarcar una amplia gama de escalas espaciales. Apéndice B se resumen algunas de las características importantes de las capas límite turbulentas, incluyendo el descubrimiento de que el perfil de velocidad media dentro de la capa límite turbulenta está muy cerca de una función logarítmica de la distancia desde el límite.Los parámetros que especifican el perfil se puede determinar simplemente a partir del espesor de la capa y la velocidad media de flujo.
La teoría de flujo de canal abierto se aplica esta representación matemática de una capa límite turbulenta para describir suspensión de sedimentos, el transporte, y la deposición por flujo de agua turbulento para los casos en que la anchura de la corriente es mucho mayor que la profundidad del agua. Apéndice C proporciona la derivación de una expresión matemática, la ecuación. (A9), para el sedimento capacidad de carga de una capa de agua turbulenta como una función del tamaño de las partículas de sedimento. Esta expresión se utiliza en el tratamiento numérico de cuantificar la suspensión de sedimentos del flujo de agua. La expresión requiere que la velocidad de sedimentación de partículas para cada uno de los tamaños de partícula que se supone en el modelo. Apéndice D describe cómo estas velocidades de sedimentación se pueden obtener a través de ajustes empíricos a los datos experimentales.
El énfasis de este trabajo es el uso de la modelización numérica para explorar la erosión a gran escala, el transporte de sedimentos y procesos de deposición que operaron durante el diluvio del Génesis como se infiere de los sedimentos cubriendo los continentes de hoy. Las características prominentes del registro sedimentario, como se explica en la introducción, sugieren que las láminas de agua turbulenta barriendo sobre la superficie continente deben haber jugado un papel importante. Tal movimiento de agua está en la categoría general de límite turbulenta flujo de la capa, que es de gran interés práctico y uno que se ha estudiado experimentalmente por muchos años. En la comunidad de ingeniería hidrológica, este tipo de flujo de agua se refiere al flujo de canal como abierta. Ejemplos de flujos de canal abierto incluyen los ríos, las corrientes de marea, canales de riego, y láminas de agua corriendo a través de la superficie del suelo después de una lluvia. Las ecuaciones usadas comúnmente para modelar estas corrientes están anclados en las mediciones experimentales y décadas de validación en muchas aplicaciones diversas. Es la turbulencia del agua que fluye en dichos flujos que mantiene las partículas de sedimento en suspensión. El Diario de Ingeniería Hidráulica no es sino una de varias revistas que se ha publicado una gran cantidad de documentos en el flujo de canal abierto turbulento y el transporte de sedimentos en las últimas décadas.
Apéndice A se resumen las observaciones, experimentos, y los esfuerzos para formular una descripción matemática de la turbulencia del fluido en los dos últimos siglos. Una descripción de flujo de fluido turbulento proporcionado hace casi un siglo por el científico británico LF Richardson (1920) sigue siendo válida hoy en día. Su descripción es un flujo cuyos movimientos se caracterizan por una jerarquía de vórtices, o remolinos, de grande a pequeño. Estos remolinos, incluidas las grandes, son inestables. La cizalla que su rotación ejerce sobre el fluido que rodea genera más pequeñas nuevas remolinos. La energía cinética de los remolinos grandes se pasa así a los remolinos más pequeños que surgen de ellos. Estos remolinos más pequeños a su vez se someten a un mismo proceso, dando lugar a remolinos aún más pequeñas que heredan la energía de sus predecesores, y así sucesivamente. De esta manera, la energía se transmite de las grandes escalas de movimiento a escalas más y más pequeños hasta alcanzar una escala de longitud suficientemente pequeño que la viscosidad molecular del fluido transforma la energía cinética de estos remolinos más pequeños en calor.
Cuando un fluido se está moviendo con respecto a una superficie fija, la velocidad del fluido, comenzando desde cero en el límite, los aumentos-primeros rápidamente, y luego menos rápidamente-como la distancia desde la superficie aumenta. La región adyacente a la superficie en la que la velocidad media del flujo paralelo a la superficie aún está cambiando, al menos modestamente, ya que uno se aleja de la superficie es conocida como la capa límite. Cuando la velocidad del fluido sobre la superficie es suficientemente alta, la capa límite se vuelve turbulento y se llena de remolinos que pueden abarcar una amplia gama de escalas espaciales. Apéndice B se resumen algunas de las características importantes de las capas límite turbulentas, incluyendo el descubrimiento de que el perfil de velocidad media dentro de la capa límite turbulenta está muy cerca de una función logarítmica de la distancia desde el límite.Los parámetros que especifican el perfil se puede determinar simplemente a partir del espesor de la capa y la velocidad media de flujo.
La teoría de flujo de canal abierto se aplica esta representación matemática de una capa límite turbulenta para describir suspensión de sedimentos, el transporte, y la deposición por flujo de agua turbulento para los casos en que la anchura de la corriente es mucho mayor que la profundidad del agua. Apéndice C proporciona la derivación de una expresión matemática, la ecuación. (A9), para el sedimento capacidad de carga de una capa de agua turbulenta como una función del tamaño de las partículas de sedimento. Esta expresión se utiliza en el tratamiento numérico de cuantificar la suspensión de sedimentos del flujo de agua. La expresión requiere que la velocidad de sedimentación de partículas para cada uno de los tamaños de partícula que se supone en el modelo. Apéndice D describe cómo estas velocidades de sedimentación se pueden obtener a través de ajustes empíricos a los datos experimentales.
Fuente del sedimento
Obviamente, un tema importante en la formación del registro sedimentario de la tierra es el origen de los sedimentos.Desde el disco de rock, está claro que había antes de las inundaciones sedimentos continentales. Sin embargo, en aras de la simplicidad, estos sedimentos se tienen en cuenta en los ejemplos ilustrativos que presentamos. En lugar de ello, se supone que el sedimento depositado durante la inundación se deriva de toda erosión de roca de fondo continental durante la propia Flood. En cuanto a los procesos erosivos, restringimos nuestro alcance al mecanismo de cavitación, de nuevo por simplicidad. Suponemos que las contribuciones de otros procesos eran pequeñas en comparación.Asumimos además que la erosión por cavitación de los resultados de la roca de fondo continentales cristalinas en una distribución de tamaños de partícula correspondiente al 70% de arena fina, 20% de arena de medio, y 10% de arena gruesa. Aquí la fracción de arena fina también incluye la arcilla y limo, que se supone para flocular para formar partículas que muestran sedimentación comportamiento idéntico al de arena fina. La media de los diámetros de partícula de estas tres clases de tamaño son de 0,063 mm (0,0025 pulgadas), 0,25 mm (0,010 pulgadas) y 1 mm (0,039 in), respectivamente. En este modelo descuidamos carbonatos, que en el registro real de la roca representan del orden del 30% del volumen total de sedimentos.
Reconocemos que es difícil imaginar cómo feldespato, incluso cuando se reduce por cavitación a 0,063 mm (0,0025 pulgadas) tamaños de partículas y más pequeño, podría ser transformado a los minerales de arcilla en el lapso de tiempo breve disponible durante la inundación. Reconocemos que una parte importante de la arcilla en las pizarras y esquistos de barro en el registro sedimentario fanerozoico bien puede haber sido derivado de pizarras y esquistos de barro de la tierra antes de la inundación. Por ejemplo, los estratos inclinados Precámbrico expuesta en la garganta interior del Gran Cañón, las rocas que incluyen el Grupo Unkar, la Formación Nankoweap, y el Grupo Chuar, mostrar espesores totales de cerca de dos millas, la mayoría de pizarra y piedra caliza (Austin 1994) . Aún más impresionante, el Mesoproterozoico (Precámbrico) Cinturón supergrupo, expuesta en el oeste de Montana, Idaho, Wyoming, Washington y Columbia Británica, es en su mayoría lutolita (pizarra, arena fina, y carbonato) y hasta 8 millas (12,8 km) de espesor (Winston y Link 1993). Estos ejemplos sugieren que puede haber habido una gran cantidad de mudrocks en la tierra antes de la inundación, posiblemente suficiente para dar cuenta de la mayor parte de la arcilla y rocas carbonatadas en el registro sedimentario de inundación. La exploración de las consecuencias de las condiciones iniciales que incluyen una capa considerable de sedimentos lutolita pre-inundación es una tarea atractiva para la futura aplicación de este modelo.
Apéndice E proporciona una descripción del submodelo cavitación. Se implementa en el código numérico por medio de la ecuación. (A11). Tenga en cuenta que este tratamiento de cavitación incluye una velocidad umbral de cavitación de 15 m / s por debajo del cual no cavitación, y por lo tanto no la erosión, se produce. Apéndice E también se describen los criterios para la deposición y de la erosión de los sedimentos ya depositados.
Teniendo en cuenta que el grosor medio de los sedimentos de inundación en los continentes es hoy en día cerca de 1800 m (5905 pies), no es de extrañar que un modelo numérico capaz de erosionar, transportar y depositar esa cantidad de sedimentos dará lugar a espesores de sedimentos en algunos lugares que exceden significativamente de que el valor promedio. En las primeras pruebas se encontró que los cálculos se hacen inestables a menos que se permite algún grado de compensación isostática en lugares donde los espesores de sedimentos se vuelven grandes.Apéndice F describe cómo la compensación isostática se incluye. simétrica compensación se aplica para las cargas negativas que se derivan de la erosión del lecho de roca.
Para describir el flujo de agua sobre la tierra de una manera cuantitativa, el modelo numérico hace uso de lo que se conoce como la aproximación aguas poco profundas. Esta aproximación requiere que la profundidad del agua en todas partes sea pequeña en comparación con las escalas horizontales de interés. La profundidad de las cuencas oceánicas hoy-y, presumiblemente, también durante la inundación-es de aproximadamente 4 km (2,5 millas). Por el contrario, el punto de la cuadrícula espaciado horizontal de la parrilla de cálculo para los casos que describimos en este artículo es de unos 120 km (74,5 millas). Las profundidades del mar prevista sobre las regiones continentales, donde se encuentra nuestro principal interés, sin embargo, son mucho más pequeños que los de las cuencas oceánicas. Por lo tanto la aproximación aguas poco profundas es totalmente apropiado para este problema. Esa aproximación permite que el flujo de agua sobre la superficie del globo que se describe en términos de una sola capa de agua con espesor lateralmente variable. Lo que de otro modo sería un costoso problema tridimensional se convierte ahora en uno de dos dimensiones mucho más manejable.
Apéndice G describe el enfoque matemático para resolver de la velocidad del agua y la altura del agua sobre la superficie de la tierra, como una función del tiempo. El enfoque implica la resolución de lo que se conoce como las ecuaciones de aguas poco profundas en una esfera giratoria. Estas son las Ecs. (A12) y (A14) en el Apéndice G. Ellos expresan, respectivamente, la conservación de la masa y la conservación del momento lineal. Se resuelven de una manera discreta usando lo que se conoce como un enfoque semi-lagrangiano sobre una malla construida a partir del icosaedro regular como se muestra en la Fig. 1.
Un sistema esférico de coordenadas se define por separado en cada punto de la cuadrícula en la malla de tal manera que el ecuador del sistema de coordenadas pasa a través del punto de la cuadrícula y los ejes de longitud y latitud locales están alineados con el este global y direcciones norte. El enfoque semi-lagrangiano, debido a sus bajos niveles de difusión numérica, también se utiliza para el transporte de sedimentos horizontal. Siete capas de espesor fijo se utilizan para resolver la concentración de sedimentos en la dirección vertical, con capas más delgadas en la parte inferior y las capas más gruesas en la parte superior de la columna. Estos mismos métodos numéricos se han aplicado y validado en uno de los modelos de predicción numérica del tiempo más destacados del mundo, un modelo conocido como GME desarrollado por el Servicio Meteorológico de Alemania a finales de 1990 (Majewski et al., 2002).
El movimiento del agua es impulsado por tsunamis de gran amplitud que se generan a lo largo de los segmentos de la zona de subducción como la placa subducting y placa superior, de una manera cíclica, de bloqueo y luego libere repentinamente y deslice rápidamente una sobre otra. Mientras que las dos placas adyacentes están bloqueadas, el fondo del mar es arrastrado hacia abajo por la placa litosférica se hunde de forma constante por debajo. Cuando las placas se desbloquean, el fondo del mar se recupera rápidamente, generando un tsunami de gran amplitud. Para los casos que se muestran en este documento, las zonas de subducción se colocan a lo largo de los meridianos, entre las latitudes 60 ° N y 60 ° S, en longitudes de -126 ° y 126 °. Estas longitudes se eligen para explotar las simetrías de la cuadrícula. El intervalo de 120 ° a lo largo de cada uno de los dos meridianos se divide en ocho 15 ° segmentos.Subduction se supone que se producen a lo largo de todos estos segmentos a una velocidad de alrededor de 2 m / s en un ángulo de 45 °. Mientras que las placas en la zona de subducción están bloqueadas, el fondo marino a lo largo de cada uno de los segmentos se supone que se mueve hacia abajo a una velocidad de aproximadamente 2 sin (45 °) = 1,4 m / s debido al movimiento constante a la baja de la losa lithospheric subducting debajo. En cada paso de tiempo de 240 s, uno de los 16 segmentos se permite para desbloquear y deslizarse, permitiendo que el fondo de la zanja de recuperarse a su altura nominal, no presionada. La amplitud de la recuperación del fondo de la zanja es de aproximadamente 1,4 m / s × 16 × 240 s = 5400 m (17.716 pies). Este levantamiento impulsiva del segmento del fondo de la zanja 15 ° inicia un tsunami que viaja a través de la 4000 m (13.123 pies) de profundidad del océano a una velocidad de unos 200 m / s.
Fig. 2 muestra un par de instantáneas, en los momentos de 4,8 horas y 9,6 horas desde el comienzo del cálculo, de las perturbaciones de la altura de la superficie del agua generada por los rebotes sucesivos del fondo del mar en la zona de subducción situada a lo largo del meridiano a 126 ° longitud. Un tren similar de alteraciones del tsunami se genera en la zona de subducción situada a lo largo del meridiano situado a -126 ° de longitud. En este cálculo no es el continente en la forma de un casquete esférico a la izquierda de la línea vertical.
Otras distribuciones de zona de subducción se examinaron, incluyendo una sola zona a lo largo del meridiano a 180 ° de longitud, y también una sola zona a lo largo del ecuador desde 90 ° a 270 ° de longitud. Las otras distribuciones dieron resultados cualitativamente similares a las de los casos ilustrativos se presentan a continuación.
Obviamente, un tema importante en la formación del registro sedimentario de la tierra es el origen de los sedimentos.Desde el disco de rock, está claro que había antes de las inundaciones sedimentos continentales. Sin embargo, en aras de la simplicidad, estos sedimentos se tienen en cuenta en los ejemplos ilustrativos que presentamos. En lugar de ello, se supone que el sedimento depositado durante la inundación se deriva de toda erosión de roca de fondo continental durante la propia Flood. En cuanto a los procesos erosivos, restringimos nuestro alcance al mecanismo de cavitación, de nuevo por simplicidad. Suponemos que las contribuciones de otros procesos eran pequeñas en comparación.Asumimos además que la erosión por cavitación de los resultados de la roca de fondo continentales cristalinas en una distribución de tamaños de partícula correspondiente al 70% de arena fina, 20% de arena de medio, y 10% de arena gruesa. Aquí la fracción de arena fina también incluye la arcilla y limo, que se supone para flocular para formar partículas que muestran sedimentación comportamiento idéntico al de arena fina. La media de los diámetros de partícula de estas tres clases de tamaño son de 0,063 mm (0,0025 pulgadas), 0,25 mm (0,010 pulgadas) y 1 mm (0,039 in), respectivamente. En este modelo descuidamos carbonatos, que en el registro real de la roca representan del orden del 30% del volumen total de sedimentos.
Reconocemos que es difícil imaginar cómo feldespato, incluso cuando se reduce por cavitación a 0,063 mm (0,0025 pulgadas) tamaños de partículas y más pequeño, podría ser transformado a los minerales de arcilla en el lapso de tiempo breve disponible durante la inundación. Reconocemos que una parte importante de la arcilla en las pizarras y esquistos de barro en el registro sedimentario fanerozoico bien puede haber sido derivado de pizarras y esquistos de barro de la tierra antes de la inundación. Por ejemplo, los estratos inclinados Precámbrico expuesta en la garganta interior del Gran Cañón, las rocas que incluyen el Grupo Unkar, la Formación Nankoweap, y el Grupo Chuar, mostrar espesores totales de cerca de dos millas, la mayoría de pizarra y piedra caliza (Austin 1994) . Aún más impresionante, el Mesoproterozoico (Precámbrico) Cinturón supergrupo, expuesta en el oeste de Montana, Idaho, Wyoming, Washington y Columbia Británica, es en su mayoría lutolita (pizarra, arena fina, y carbonato) y hasta 8 millas (12,8 km) de espesor (Winston y Link 1993). Estos ejemplos sugieren que puede haber habido una gran cantidad de mudrocks en la tierra antes de la inundación, posiblemente suficiente para dar cuenta de la mayor parte de la arcilla y rocas carbonatadas en el registro sedimentario de inundación. La exploración de las consecuencias de las condiciones iniciales que incluyen una capa considerable de sedimentos lutolita pre-inundación es una tarea atractiva para la futura aplicación de este modelo.
Apéndice E proporciona una descripción del submodelo cavitación. Se implementa en el código numérico por medio de la ecuación. (A11). Tenga en cuenta que este tratamiento de cavitación incluye una velocidad umbral de cavitación de 15 m / s por debajo del cual no cavitación, y por lo tanto no la erosión, se produce. Apéndice E también se describen los criterios para la deposición y de la erosión de los sedimentos ya depositados.
Teniendo en cuenta que el grosor medio de los sedimentos de inundación en los continentes es hoy en día cerca de 1800 m (5905 pies), no es de extrañar que un modelo numérico capaz de erosionar, transportar y depositar esa cantidad de sedimentos dará lugar a espesores de sedimentos en algunos lugares que exceden significativamente de que el valor promedio. En las primeras pruebas se encontró que los cálculos se hacen inestables a menos que se permite algún grado de compensación isostática en lugares donde los espesores de sedimentos se vuelven grandes.Apéndice F describe cómo la compensación isostática se incluye. simétrica compensación se aplica para las cargas negativas que se derivan de la erosión del lecho de roca.
Para describir el flujo de agua sobre la tierra de una manera cuantitativa, el modelo numérico hace uso de lo que se conoce como la aproximación aguas poco profundas. Esta aproximación requiere que la profundidad del agua en todas partes sea pequeña en comparación con las escalas horizontales de interés. La profundidad de las cuencas oceánicas hoy-y, presumiblemente, también durante la inundación-es de aproximadamente 4 km (2,5 millas). Por el contrario, el punto de la cuadrícula espaciado horizontal de la parrilla de cálculo para los casos que describimos en este artículo es de unos 120 km (74,5 millas). Las profundidades del mar prevista sobre las regiones continentales, donde se encuentra nuestro principal interés, sin embargo, son mucho más pequeños que los de las cuencas oceánicas. Por lo tanto la aproximación aguas poco profundas es totalmente apropiado para este problema. Esa aproximación permite que el flujo de agua sobre la superficie del globo que se describe en términos de una sola capa de agua con espesor lateralmente variable. Lo que de otro modo sería un costoso problema tridimensional se convierte ahora en uno de dos dimensiones mucho más manejable.
Apéndice G describe el enfoque matemático para resolver de la velocidad del agua y la altura del agua sobre la superficie de la tierra, como una función del tiempo. El enfoque implica la resolución de lo que se conoce como las ecuaciones de aguas poco profundas en una esfera giratoria. Estas son las Ecs. (A12) y (A14) en el Apéndice G. Ellos expresan, respectivamente, la conservación de la masa y la conservación del momento lineal. Se resuelven de una manera discreta usando lo que se conoce como un enfoque semi-lagrangiano sobre una malla construida a partir del icosaedro regular como se muestra en la Fig. 1.
Un sistema esférico de coordenadas se define por separado en cada punto de la cuadrícula en la malla de tal manera que el ecuador del sistema de coordenadas pasa a través del punto de la cuadrícula y los ejes de longitud y latitud locales están alineados con el este global y direcciones norte. El enfoque semi-lagrangiano, debido a sus bajos niveles de difusión numérica, también se utiliza para el transporte de sedimentos horizontal. Siete capas de espesor fijo se utilizan para resolver la concentración de sedimentos en la dirección vertical, con capas más delgadas en la parte inferior y las capas más gruesas en la parte superior de la columna. Estos mismos métodos numéricos se han aplicado y validado en uno de los modelos de predicción numérica del tiempo más destacados del mundo, un modelo conocido como GME desarrollado por el Servicio Meteorológico de Alemania a finales de 1990 (Majewski et al., 2002).
El movimiento del agua es impulsado por tsunamis de gran amplitud que se generan a lo largo de los segmentos de la zona de subducción como la placa subducting y placa superior, de una manera cíclica, de bloqueo y luego libere repentinamente y deslice rápidamente una sobre otra. Mientras que las dos placas adyacentes están bloqueadas, el fondo del mar es arrastrado hacia abajo por la placa litosférica se hunde de forma constante por debajo. Cuando las placas se desbloquean, el fondo del mar se recupera rápidamente, generando un tsunami de gran amplitud. Para los casos que se muestran en este documento, las zonas de subducción se colocan a lo largo de los meridianos, entre las latitudes 60 ° N y 60 ° S, en longitudes de -126 ° y 126 °. Estas longitudes se eligen para explotar las simetrías de la cuadrícula. El intervalo de 120 ° a lo largo de cada uno de los dos meridianos se divide en ocho 15 ° segmentos.Subduction se supone que se producen a lo largo de todos estos segmentos a una velocidad de alrededor de 2 m / s en un ángulo de 45 °. Mientras que las placas en la zona de subducción están bloqueadas, el fondo marino a lo largo de cada uno de los segmentos se supone que se mueve hacia abajo a una velocidad de aproximadamente 2 sin (45 °) = 1,4 m / s debido al movimiento constante a la baja de la losa lithospheric subducting debajo. En cada paso de tiempo de 240 s, uno de los 16 segmentos se permite para desbloquear y deslizarse, permitiendo que el fondo de la zanja de recuperarse a su altura nominal, no presionada. La amplitud de la recuperación del fondo de la zanja es de aproximadamente 1,4 m / s × 16 × 240 s = 5400 m (17.716 pies). Este levantamiento impulsiva del segmento del fondo de la zanja 15 ° inicia un tsunami que viaja a través de la 4000 m (13.123 pies) de profundidad del océano a una velocidad de unos 200 m / s.
Fig. 2 muestra un par de instantáneas, en los momentos de 4,8 horas y 9,6 horas desde el comienzo del cálculo, de las perturbaciones de la altura de la superficie del agua generada por los rebotes sucesivos del fondo del mar en la zona de subducción situada a lo largo del meridiano a 126 ° longitud. Un tren similar de alteraciones del tsunami se genera en la zona de subducción situada a lo largo del meridiano situado a -126 ° de longitud. En este cálculo no es el continente en la forma de un casquete esférico a la izquierda de la línea vertical.
Otras distribuciones de zona de subducción se examinaron, incluyendo una sola zona a lo largo del meridiano a 180 ° de longitud, y también una sola zona a lo largo del ecuador desde 90 ° a 270 ° de longitud. Las otras distribuciones dieron resultados cualitativamente similares a las de los casos ilustrativos se presentan a continuación.
Un caso ilustrativo
Para ilustrar los patrones globales de sedimentos elegimos una geometría simple de un solo continente circular, centrada en el ecuador y la longitud cero, que cubre el 38% de la superficie de la tierra. El fondo del océano que rodea el continente se considera que tiene una altura uniforme de -4000 m (-13,123 pies) con respecto al nivel medio del mar. La altura del continente en su centro se encuentra a 100 m (328 pies) con respecto al nivel medio del mar y disminuye suavemente a -72 m (-236 pies) en su borde. Inicialmente, el agua está en reposo con su superficie a nivel del mar. La superficie de los continentes se asume todas partes consistir en lecho de roca cristalina. La tierra se supone que está girando a su velocidad de rotación actual.
Una característica sorprendente en el patrón de flujo de agua emerge muy temprano en el cálculo con este modelo.Fig. La figura 3 muestra la altura de la superficie del agua en los momentos de 2,5 y 5,0 días, visto desde cuatro puntos separados a 90 ° por encima del ecuador. Especialmente sorprendente es la notable elevación de la altura de la superficie del agua en relación con el nivel del mar por encima de la mayor parte del continente en la Fig. 3 (a) y la Fig.3 (b) revelar. La mayor elevación de la superficie del agua se produce dentro de los grandes giros anticiclónicos en el patrón de flujo de agua en las latitudes altas. Estos giros son análogas a las circulaciones de alta presión (altos) en latitudes medias y altas de la atmósfera, los sistemas que giran en sentido antihorario en el hemisferio norte y hacia la derecha en el sur. La constante acumulación de agua en el continente superficie, al menos hasta que se pueda un estado de equilibrio alcanzado, es una consecuencia de los tsunamis que llevan el agua hacia el continente a una velocidad más alta que pueda drenarse de nuevo en el océano a través de la influencia de la gravedad. Los giros anti-ciclónicos son la consecuencia del efecto Coriolis que contribuye una fuerza perpendicular a la dirección del flujo de agua, es decir, hacia el centro del giro (la - f k × u término de la ecuación A14.). Esta fuerza actúa para equilibrar la fuerza del gradiente de presión que actúa en la dirección hacia fuera desde el centro del giro (el término h † g ∇ en la Ec. A14) debido a la altura del agua allí. La magnitud del efecto de Coriolis, que varía con el seno de la latitud, es cero en el ecuador y máxima en los polos. En este ejemplo, el efecto Coriolis ejerce claramente una influencia importante en el patrón general de flujo de agua por encima de la superficie continental.
Por otra parte, parcelas en la Fig. 3 (c) - (f) revelan que cuatro fuertes giros ciclónicos también surgen en las latitudes altas del hemisferio oceánico. Estos giros, análogos a los sistemas de baja presión en la atmósfera, giran en la dirección hacia la derecha en el hemisferio norte y en el sentido antihorario en el hemisferio sur. En este cálculo, que están asociados con una depresión significativa de la superficie del océano. A los cinco días, tal como se indica en las parcelas (d) y (f), esta disminución de la superficie del océano en los centros de los giros supera los 1000 m (3280 pies) por debajo del nivel medio del mar.
En el momento de cinco días el patrón de flujo se aproxima a la condición en la que la cantidad de agua emplazado en el continente por los tsunamis se equilibra con la escorrentía de los niveles elevados de agua en el continente. Debido a que el efecto de Coriolis es menor en las latitudes bajas, la mayor parte de la segunda vuelta se produce en estas latitudes más bajas, como es evidente en la figura. 3. Esta segunda vuelta también da lugar a la erosión de la roca madre notable, ya que la línea de contorno negro denota una elevación de la superficie del continente -300 -984 m (pies) indica en parcelas (d) y (h). El patrón de flujo general establecido por el tiempo de cinco días se encontró a persistir a lo largo del período de 150 días asumido para el intervalo en el que las aguas subieron durante la inundación.
Fig. 3 también muestra el tipo de velocidades de la columna de agua que surgen por encima de la superficie del continente. En las parcelas en cinco días, las velocidades de columna trazados han sido limitados en amplitud a 50 m / s. Aplicando los criterios de la turbulencia del fluido desarrollado anteriormente, se encuentra que las profundidades de agua y velocidades de columna de agua implican que esencialmente todas partes sobre el continente el flujo es en el régimen fuertemente turbulento. Por lo tanto, tiene la capacidad de transportar una carga de sedimentos considerable. Durante gran parte del continente, especialmente a lo largo de sus márgenes, la velocidad en la base de la columna de agua excede significativamente la velocidad umbral de cavitación y por lo tanto se da a entender una erosión significativa. El sedimento producido a partir de la erosión del lecho de roca se suspende fácilmente en el flujo turbulento. Dondequiera que la carga de sedimentos es superior al 10% en volumen en la capa basal, se produce la deposición de sedimentos. Una vez que una capa de sedimento está presente, es vulnerable a ser erosionado, suspendido, y transportado antes de ser depositado de nuevo en otro lugar. la erosión del lecho rocoso y la deposición de sedimentos generan relieve topográfico de la superficie continental, compensación que también afecta el patrón de flujo de agua.
Fig. 4 intentos de proporcionar una visión general de la erosión, transporte y sedimentación que se desarrolla en un lapso de 100 días en este modelo. Utiliza pares instantáneas, en tiempos de 50 y 100 días, mostrando por medio del color, respectivamente, (i) la altura de la superficie del agua por encima del nivel del mar inicial, (ii) la profundidad del agua, (iii) la erosión del lecho de roca acumulada, (iv ) el grosor instantáneo de sedimento en suspensión por el flujo turbulento, (v) la cantidad acumulada neto de sedimento que queda en la superficie como resultado de los procesos en curso de deposición y erosión, y (vi) la topografía de la superficie continental como la erosión y deposición y la compensación isostática actúan conjuntamente para alterarlo. Las flechas en todas las parcelas de la Fig. 4 representan las velocidades del agua en la parte inferior de la columna de agua por encima de la superficie de la tierra.Para mayor claridad, las velocidades de agua han sido recortado a 30 m / s. Como referencia, la velocidad del agua para el inicio de la cavitación es de 15 m / s. La vigorosa y altamente turbulento flujo de agua, cuya energía es mantenida por los tsunamis, es suficiente para suspender más de 150 m (492 pies) de sedimentos cerca de los centros de los patrones de flujo circulares en las latitudes altas y varias decenas de metros más otros lugares por encima del continente como se indica en la figura. 4 (g). A medida que las profundidades de sedimento depositado convertido en gran más allá de 50 días, la cantidad de sedimentos en suspensión disminuye, como se observa en la Fig. 4 (h). Sin embargo, el agua turbulenta transporta cantidades muy abundantes de sedimento erosionado por miles de kilómetros a través de la superficie del continente.
Las parcelas (a) y (b) de la figura. 4 muestran que la sorprendente inundación de la superficie continental observó a los 5 días de la Fig. 3 persiste hasta 100 días. La altura de la superficie del agua supera los 1500 m (4921 pies) por encima del nivel medio del mar en las altas latitudes giros anticiclónicos y generalmente es superior a 500 m (1640 pies) sobre el nivel medio del mar en otro lugar. En contraste con las parcelas en las Figs. 4 (a) y (b) que muestran la altura de la superficie del agua, las parcelas en las Figs. 4 (c) y (d) muestran la profundidad real del agua hasta la superficie de los continentes. Cuando la superficie está por debajo del nivel medio del mar, la profundidad del agua se establece en cero. En otras palabras, estas parcelas muestran la profundidad del agua sólo cuando la superficie de la tierra está por encima del nivel del mar. Hay varias características notables en la fig. 4 (c) y (d). En primer lugar, mientras que la profundidad del agua son apreciables cerca del centro de los giros en 50 días, estas regiones han sido significativamente lleno de sedimento por 100 días de tal manera que el agua profundidades hay notablemente más pequeño. En segundo lugar, a lo largo de los márgenes de los giros hay zonas de aguas muy poco profundas. Como puede comprobarse en las figuras. 4 (i) y (j), se trata de zonas de deposición de sedimentos de espesor. Estas zonas representan regiones donde la superficie de la tierra podría haber sido expuestas en varios momentos durante el cataclismo. Además de las zonas a lo largo de las márgenes de los giros, hay manchas en forma de cúpula aislados que puedan haber resultado lo que se conoce hoy en día como las cuencas sedimentarias. Dos de esos puntos son evidentes en la figura. 4 (i) aproximadamente a -30 ° latitud y -15 ° y -30 ° de longitud. Ambos son del orden de unos pocos cientos de kilómetros de diámetro. Después de la inundación el exceso de peso de estos enormes montículos de sedimento tendría tanto la superficie de la corteza deprimida por debajo de ellos, así como el manto subyacente.
Parcelas en las Figs. 4 (e) y (f) revelan que la mayor parte del lecho de roca erosión se produce a lo largo del margen continente.Dado que en el modelo de cavitación la velocidad de erosión varía como la sexta potencia de la diferencia entre la velocidad del agua y la velocidad de aparición de cavitación, no es sorprendente para la erosión sea más intensa en el margen continental, donde los tsunamis se encuentran con una disminución abrupta en la profundidad del agua y la velocidad del agua aumenta dramáticamente. La línea de contorno a lo largo del perímetro del continente marca la profundidad de 300 m (984 pies) bajo el nivel del mar. Tenga en cuenta que la más intensa erosión es oceanward de esta curva de nivel -300 m (-984 pies). El volumen acumulado de la erosión del lecho de roca es suficiente para cubrir la superficie de todo el continente con sedimentos a una profundidad media de 670 m (2.198 pies) después de 50 días y 1.109 m (3638 pies) después de 100 días, lo que refleja una erosión media (y deposición ) tasa de más de 100 días de aproximadamente 11 m / día.
Parcelas en las Figs. 4 (g) y (h) muestran las cantidades de sedimentos en suspensión en el agua turbulenta. El promedio en toda la superficie continente es de 49 m (160 pies) a los 50 días y 26 m (85 pies) a 100 días. Las mayores cantidades se encuentran cerca de los centros de los giros, donde la profundidad de la columna de agua es mayor.Parcelas en las Figs. 4 (i) y (j) mostrará el resultado neto acumulado de la deposición de sedimentos y la erosión de sedimentos. Parcelas en las Figs. 4 (k) y (l) revelan cómo la topografía continente se ve alterada por los procesos de erosión, transporte de sedimentos, la deposición de sedimentos, y el ajuste isostático parcial. La cantidad de ajuste isostático se puede estimar mediante la comparación de las parcelas en la Fig. 4 de la erosión acumulativa (e, f) y de la sedimentación neta acumulada (i, j) con la expresión resultante topográfico (k, l).
Cabe destacar la eficacia de los tsunamis y la dinámica del agua asociados a emplazar cientos de metros de sedimentos en la parte superior del continente , por encima del nivel medio del mar. Si Génesis 07:24 que dice: "Y el agua se impuso sobre la tierra ciento cincuenta días," implica que la sedimentación primaria de la inundación se extendió por 150 días, a continuación, una velocidad de sedimentación media de 12 m / día (39,3 pies / día ) sobre que las cuentas de intervalo para los aproximadamente 1800 m (5905 pies) de sedimentos, en promedio, que reside actualmente en los continentes. Las tasas medias obtenidas en este cálculo ilustrativo a continuación, no son demasiado lejos del valor medio inferirse del texto de Génesis.
Fig.5 proporciona una imagen más detallada del sedimento en suspensión y depositado cuando se separa en las tres clases de sedimentos asumidos. Como se mencionó anteriormente suponemos que los procesos de erosión, especialmente cavitación, reducen lecho de roca cristalina en una mezcla de partículas relativamente finas, 70% con un diámetro medio de 0,063 mm (0,0025 in) correspondiente a la de arena fina, 20% con un diámetro medio de 0,25 mm (0,010 in) correspondiente a arena media, y 10% con un diámetro medio de 1 mm (0,039 in) correspondiente a la arena gruesa. Fig.5 muestra la distribución lateral de sedimentos en suspensión para cada una de estas clases de tamaño en un tiempo de 50 días. También muestra la distribución lateral de los sedimentos depositados por clase de tamaño a esta misma hora. La arena gruesa tiene una velocidad de sedimentación mucho más alta que la arena fina y medio. Por tanto, es más difícil de mantener en suspensión, como la Fig. 5 (e) revela. También es la primera a caer de suspensión como la velocidad de flujo disminuye. Por tanto, la arena gruesa tiende a depositarse más cerca de su fuente como se indica en la figura. 5 (f).
Para ilustrar los patrones globales de sedimentos elegimos una geometría simple de un solo continente circular, centrada en el ecuador y la longitud cero, que cubre el 38% de la superficie de la tierra. El fondo del océano que rodea el continente se considera que tiene una altura uniforme de -4000 m (-13,123 pies) con respecto al nivel medio del mar. La altura del continente en su centro se encuentra a 100 m (328 pies) con respecto al nivel medio del mar y disminuye suavemente a -72 m (-236 pies) en su borde. Inicialmente, el agua está en reposo con su superficie a nivel del mar. La superficie de los continentes se asume todas partes consistir en lecho de roca cristalina. La tierra se supone que está girando a su velocidad de rotación actual.
Una característica sorprendente en el patrón de flujo de agua emerge muy temprano en el cálculo con este modelo.Fig. La figura 3 muestra la altura de la superficie del agua en los momentos de 2,5 y 5,0 días, visto desde cuatro puntos separados a 90 ° por encima del ecuador. Especialmente sorprendente es la notable elevación de la altura de la superficie del agua en relación con el nivel del mar por encima de la mayor parte del continente en la Fig. 3 (a) y la Fig.3 (b) revelar. La mayor elevación de la superficie del agua se produce dentro de los grandes giros anticiclónicos en el patrón de flujo de agua en las latitudes altas. Estos giros son análogas a las circulaciones de alta presión (altos) en latitudes medias y altas de la atmósfera, los sistemas que giran en sentido antihorario en el hemisferio norte y hacia la derecha en el sur. La constante acumulación de agua en el continente superficie, al menos hasta que se pueda un estado de equilibrio alcanzado, es una consecuencia de los tsunamis que llevan el agua hacia el continente a una velocidad más alta que pueda drenarse de nuevo en el océano a través de la influencia de la gravedad. Los giros anti-ciclónicos son la consecuencia del efecto Coriolis que contribuye una fuerza perpendicular a la dirección del flujo de agua, es decir, hacia el centro del giro (la - f k × u término de la ecuación A14.). Esta fuerza actúa para equilibrar la fuerza del gradiente de presión que actúa en la dirección hacia fuera desde el centro del giro (el término h † g ∇ en la Ec. A14) debido a la altura del agua allí. La magnitud del efecto de Coriolis, que varía con el seno de la latitud, es cero en el ecuador y máxima en los polos. En este ejemplo, el efecto Coriolis ejerce claramente una influencia importante en el patrón general de flujo de agua por encima de la superficie continental.
Por otra parte, parcelas en la Fig. 3 (c) - (f) revelan que cuatro fuertes giros ciclónicos también surgen en las latitudes altas del hemisferio oceánico. Estos giros, análogos a los sistemas de baja presión en la atmósfera, giran en la dirección hacia la derecha en el hemisferio norte y en el sentido antihorario en el hemisferio sur. En este cálculo, que están asociados con una depresión significativa de la superficie del océano. A los cinco días, tal como se indica en las parcelas (d) y (f), esta disminución de la superficie del océano en los centros de los giros supera los 1000 m (3280 pies) por debajo del nivel medio del mar.
En el momento de cinco días el patrón de flujo se aproxima a la condición en la que la cantidad de agua emplazado en el continente por los tsunamis se equilibra con la escorrentía de los niveles elevados de agua en el continente. Debido a que el efecto de Coriolis es menor en las latitudes bajas, la mayor parte de la segunda vuelta se produce en estas latitudes más bajas, como es evidente en la figura. 3. Esta segunda vuelta también da lugar a la erosión de la roca madre notable, ya que la línea de contorno negro denota una elevación de la superficie del continente -300 -984 m (pies) indica en parcelas (d) y (h). El patrón de flujo general establecido por el tiempo de cinco días se encontró a persistir a lo largo del período de 150 días asumido para el intervalo en el que las aguas subieron durante la inundación.
Fig. 3 también muestra el tipo de velocidades de la columna de agua que surgen por encima de la superficie del continente. En las parcelas en cinco días, las velocidades de columna trazados han sido limitados en amplitud a 50 m / s. Aplicando los criterios de la turbulencia del fluido desarrollado anteriormente, se encuentra que las profundidades de agua y velocidades de columna de agua implican que esencialmente todas partes sobre el continente el flujo es en el régimen fuertemente turbulento. Por lo tanto, tiene la capacidad de transportar una carga de sedimentos considerable. Durante gran parte del continente, especialmente a lo largo de sus márgenes, la velocidad en la base de la columna de agua excede significativamente la velocidad umbral de cavitación y por lo tanto se da a entender una erosión significativa. El sedimento producido a partir de la erosión del lecho de roca se suspende fácilmente en el flujo turbulento. Dondequiera que la carga de sedimentos es superior al 10% en volumen en la capa basal, se produce la deposición de sedimentos. Una vez que una capa de sedimento está presente, es vulnerable a ser erosionado, suspendido, y transportado antes de ser depositado de nuevo en otro lugar. la erosión del lecho rocoso y la deposición de sedimentos generan relieve topográfico de la superficie continental, compensación que también afecta el patrón de flujo de agua.
Fig. 4 intentos de proporcionar una visión general de la erosión, transporte y sedimentación que se desarrolla en un lapso de 100 días en este modelo. Utiliza pares instantáneas, en tiempos de 50 y 100 días, mostrando por medio del color, respectivamente, (i) la altura de la superficie del agua por encima del nivel del mar inicial, (ii) la profundidad del agua, (iii) la erosión del lecho de roca acumulada, (iv ) el grosor instantáneo de sedimento en suspensión por el flujo turbulento, (v) la cantidad acumulada neto de sedimento que queda en la superficie como resultado de los procesos en curso de deposición y erosión, y (vi) la topografía de la superficie continental como la erosión y deposición y la compensación isostática actúan conjuntamente para alterarlo. Las flechas en todas las parcelas de la Fig. 4 representan las velocidades del agua en la parte inferior de la columna de agua por encima de la superficie de la tierra.Para mayor claridad, las velocidades de agua han sido recortado a 30 m / s. Como referencia, la velocidad del agua para el inicio de la cavitación es de 15 m / s. La vigorosa y altamente turbulento flujo de agua, cuya energía es mantenida por los tsunamis, es suficiente para suspender más de 150 m (492 pies) de sedimentos cerca de los centros de los patrones de flujo circulares en las latitudes altas y varias decenas de metros más otros lugares por encima del continente como se indica en la figura. 4 (g). A medida que las profundidades de sedimento depositado convertido en gran más allá de 50 días, la cantidad de sedimentos en suspensión disminuye, como se observa en la Fig. 4 (h). Sin embargo, el agua turbulenta transporta cantidades muy abundantes de sedimento erosionado por miles de kilómetros a través de la superficie del continente.
Las parcelas (a) y (b) de la figura. 4 muestran que la sorprendente inundación de la superficie continental observó a los 5 días de la Fig. 3 persiste hasta 100 días. La altura de la superficie del agua supera los 1500 m (4921 pies) por encima del nivel medio del mar en las altas latitudes giros anticiclónicos y generalmente es superior a 500 m (1640 pies) sobre el nivel medio del mar en otro lugar. En contraste con las parcelas en las Figs. 4 (a) y (b) que muestran la altura de la superficie del agua, las parcelas en las Figs. 4 (c) y (d) muestran la profundidad real del agua hasta la superficie de los continentes. Cuando la superficie está por debajo del nivel medio del mar, la profundidad del agua se establece en cero. En otras palabras, estas parcelas muestran la profundidad del agua sólo cuando la superficie de la tierra está por encima del nivel del mar. Hay varias características notables en la fig. 4 (c) y (d). En primer lugar, mientras que la profundidad del agua son apreciables cerca del centro de los giros en 50 días, estas regiones han sido significativamente lleno de sedimento por 100 días de tal manera que el agua profundidades hay notablemente más pequeño. En segundo lugar, a lo largo de los márgenes de los giros hay zonas de aguas muy poco profundas. Como puede comprobarse en las figuras. 4 (i) y (j), se trata de zonas de deposición de sedimentos de espesor. Estas zonas representan regiones donde la superficie de la tierra podría haber sido expuestas en varios momentos durante el cataclismo. Además de las zonas a lo largo de las márgenes de los giros, hay manchas en forma de cúpula aislados que puedan haber resultado lo que se conoce hoy en día como las cuencas sedimentarias. Dos de esos puntos son evidentes en la figura. 4 (i) aproximadamente a -30 ° latitud y -15 ° y -30 ° de longitud. Ambos son del orden de unos pocos cientos de kilómetros de diámetro. Después de la inundación el exceso de peso de estos enormes montículos de sedimento tendría tanto la superficie de la corteza deprimida por debajo de ellos, así como el manto subyacente.
Parcelas en las Figs. 4 (e) y (f) revelan que la mayor parte del lecho de roca erosión se produce a lo largo del margen continente.Dado que en el modelo de cavitación la velocidad de erosión varía como la sexta potencia de la diferencia entre la velocidad del agua y la velocidad de aparición de cavitación, no es sorprendente para la erosión sea más intensa en el margen continental, donde los tsunamis se encuentran con una disminución abrupta en la profundidad del agua y la velocidad del agua aumenta dramáticamente. La línea de contorno a lo largo del perímetro del continente marca la profundidad de 300 m (984 pies) bajo el nivel del mar. Tenga en cuenta que la más intensa erosión es oceanward de esta curva de nivel -300 m (-984 pies). El volumen acumulado de la erosión del lecho de roca es suficiente para cubrir la superficie de todo el continente con sedimentos a una profundidad media de 670 m (2.198 pies) después de 50 días y 1.109 m (3638 pies) después de 100 días, lo que refleja una erosión media (y deposición ) tasa de más de 100 días de aproximadamente 11 m / día.
Parcelas en las Figs. 4 (g) y (h) muestran las cantidades de sedimentos en suspensión en el agua turbulenta. El promedio en toda la superficie continente es de 49 m (160 pies) a los 50 días y 26 m (85 pies) a 100 días. Las mayores cantidades se encuentran cerca de los centros de los giros, donde la profundidad de la columna de agua es mayor.Parcelas en las Figs. 4 (i) y (j) mostrará el resultado neto acumulado de la deposición de sedimentos y la erosión de sedimentos. Parcelas en las Figs. 4 (k) y (l) revelan cómo la topografía continente se ve alterada por los procesos de erosión, transporte de sedimentos, la deposición de sedimentos, y el ajuste isostático parcial. La cantidad de ajuste isostático se puede estimar mediante la comparación de las parcelas en la Fig. 4 de la erosión acumulativa (e, f) y de la sedimentación neta acumulada (i, j) con la expresión resultante topográfico (k, l).
Cabe destacar la eficacia de los tsunamis y la dinámica del agua asociados a emplazar cientos de metros de sedimentos en la parte superior del continente , por encima del nivel medio del mar. Si Génesis 07:24 que dice: "Y el agua se impuso sobre la tierra ciento cincuenta días," implica que la sedimentación primaria de la inundación se extendió por 150 días, a continuación, una velocidad de sedimentación media de 12 m / día (39,3 pies / día ) sobre que las cuentas de intervalo para los aproximadamente 1800 m (5905 pies) de sedimentos, en promedio, que reside actualmente en los continentes. Las tasas medias obtenidas en este cálculo ilustrativo a continuación, no son demasiado lejos del valor medio inferirse del texto de Génesis.
Fig.5 proporciona una imagen más detallada del sedimento en suspensión y depositado cuando se separa en las tres clases de sedimentos asumidos. Como se mencionó anteriormente suponemos que los procesos de erosión, especialmente cavitación, reducen lecho de roca cristalina en una mezcla de partículas relativamente finas, 70% con un diámetro medio de 0,063 mm (0,0025 in) correspondiente a la de arena fina, 20% con un diámetro medio de 0,25 mm (0,010 in) correspondiente a arena media, y 10% con un diámetro medio de 1 mm (0,039 in) correspondiente a la arena gruesa. Fig.5 muestra la distribución lateral de sedimentos en suspensión para cada una de estas clases de tamaño en un tiempo de 50 días. También muestra la distribución lateral de los sedimentos depositados por clase de tamaño a esta misma hora. La arena gruesa tiene una velocidad de sedimentación mucho más alta que la arena fina y medio. Por tanto, es más difícil de mantener en suspensión, como la Fig. 5 (e) revela. También es la primera a caer de suspensión como la velocidad de flujo disminuye. Por tanto, la arena gruesa tiende a depositarse más cerca de su fuente como se indica en la figura. 5 (f).
Un segundo caso ilustrativo
El caso que acabamos de describir utiliza una distribución de los continentes que consta de una sola tapa esférica, centrada en el ecuador, que cubre 38% de la superficie del globo. Para añadir un poco más de realismo se presenta un segundo caso, que conserva los valores de los parámetros del primer caso, pero en lugar de una tapa circular utiliza una distribución continente Pangean similar. Fig.6 muestra las instantáneas a 50 y 100 días siguientes a la altura de la superficie del agua con respecto al nivel del mar (inicial) nominal (a, b); la profundidad del agua (c, d); la erosión del lecho de roca acumulada (e, f); espesor instantáneo de sedimentos en suspensión por el flujo turbulento en suspensión (g, h); deposición de sedimentos acumulados netos de (i, j); y la topografía de la superficie continental como la erosión y la deposición y la compensación isostática actuar conjuntamente alterarlo (k, l). Las flechas indican la velocidad media de columna de agua en (a, b) y agua velocidad en la base de la columna de agua en (c-l).
Este segundo caso ilustrativo muestra las mismas características destacables del primer caso incluyendo los niveles elevados de agua sobre el continente, especialmente dentro de los prominentes giros anticiclónicos en las latitudes altas y la erosión concentrados a lo largo de los márgenes continentales. El volumen acumulado de la erosión del lecho de roca es suficiente para cubrir la superficie de todo el continente con sedimentos a una profundidad media de 489 m (1.604 pies) después de 50 días y 878 m (2.880 pies) después de 100 días, lo que refleja una tasa promedio sobre el 50 día de 9,8 m / día (31,4 pies / día). Este caso demuestra cientos de metros de sedimentos emplazadas sobre el nivel del mar en la parte superior de la superficie continental, que inicialmente sí era su mayoría por encima del nivel del mar.
El caso que acabamos de describir utiliza una distribución de los continentes que consta de una sola tapa esférica, centrada en el ecuador, que cubre 38% de la superficie del globo. Para añadir un poco más de realismo se presenta un segundo caso, que conserva los valores de los parámetros del primer caso, pero en lugar de una tapa circular utiliza una distribución continente Pangean similar. Fig.6 muestra las instantáneas a 50 y 100 días siguientes a la altura de la superficie del agua con respecto al nivel del mar (inicial) nominal (a, b); la profundidad del agua (c, d); la erosión del lecho de roca acumulada (e, f); espesor instantáneo de sedimentos en suspensión por el flujo turbulento en suspensión (g, h); deposición de sedimentos acumulados netos de (i, j); y la topografía de la superficie continental como la erosión y la deposición y la compensación isostática actuar conjuntamente alterarlo (k, l). Las flechas indican la velocidad media de columna de agua en (a, b) y agua velocidad en la base de la columna de agua en (c-l).
Este segundo caso ilustrativo muestra las mismas características destacables del primer caso incluyendo los niveles elevados de agua sobre el continente, especialmente dentro de los prominentes giros anticiclónicos en las latitudes altas y la erosión concentrados a lo largo de los márgenes continentales. El volumen acumulado de la erosión del lecho de roca es suficiente para cubrir la superficie de todo el continente con sedimentos a una profundidad media de 489 m (1.604 pies) después de 50 días y 878 m (2.880 pies) después de 100 días, lo que refleja una tasa promedio sobre el 50 día de 9,8 m / día (31,4 pies / día). Este caso demuestra cientos de metros de sedimentos emplazadas sobre el nivel del mar en la parte superior de la superficie continental, que inicialmente sí era su mayoría por encima del nivel del mar.
Discusión
En el contexto de una defensa razonada de la inundación del Génesis, hay varias características principales de la superficie continental de la Tierra que reclaman una explicación. En primer lugar es el gran volumen de fosilíferos roca sedimentaria actualidad existen en la actualidad. El volumen es suficiente para cubrir la superficie continental a una profundidad media de aproximadamente 1.800 m o aproximadamente 1,1 mi. ¿Cuál fue el origen de este volumen masivo de sedimentos durante el corto lapso de tiempo de la inundación? En segundo lugar está la ubicación de este enorme volumen de sedimento. Se produce en la parte superior de los continentes, cuya superficie generalmente se encuentra por encima del nivel del mar. Esto plantea la pregunta, ¿qué tipo de proceso de agua podría concebiblemente emplazar tanto de sedimentos sobre el nivel del mar en la parte superior de la superficie de la tierra? Una tercera cuestión tiene que ver con los internos características de deposición de los sedimentos. En términos generales, la mayor parte de los sedimentos se produce como una sucesión vertical de capas horizontales, a menudo con gran extensión lateral. Tal esquema de capa-torta ordenada de los estratos lateralmente extensa se observa fácilmente, por ejemplo, por los sedimentos expuestos en las paredes del Gran Cañón. ¿Qué tipo de transporte y el proceso de deposición posiblemente podría generar tales capas uniformes sobre distancias tan grandes horizontales?
Una cuarta característica prominente de la superficie de la tierra incluye los llamados escudos continentales , incluyendo el canadiense, Báltico, Angaran (Siberia), África, India, Australia, y escudos de la Antártida. Estas grandes áreas de exposición ígneas y metamórficas del Precámbrico cristalina de alto grado rocas han experimentado una erosión significativa (a menudo con más de 1 km (0,62 millas) de roca cristalina eliminado), son casi plana, y tienen insignificante, en su caso, cubierta de sedimentos. ¿Cuándo en la historia de la tierra se produce tan intensa erosión si no fuera durante el Diluvio? Y por qué tipo de proceso?
Una quinta característica destacable es el fenómeno de las denominadas cuencas sedimentarias que cubren gran parte de las porciones no apantallado de la superficie de los continentes. Estas cuencas se describen comúnmente por la comunidad estándar de ciencias de la tierra como regiones de hundimiento a largo plazo que han proporcionado el espacio de alojamiento para el relleno con sedimentos. Frecuentes ausente de la discusión de la mayoría de las cuencas es el mecanismo responsable de su hundimiento. Sedimentos de cuenca, casi invariablemente, tienen sobre todo menores densidades que las rocas del basamento debajo. Dentro de interiores Cratón estables no hay ninguna razón obvia por la roca de densidad más baja en la superficie debe desplazar más alta densidad de la roca en la profundidad para producir hundimientos. Debido a un mecanismo convincente para el hundimiento no se ha producido en muchos contextos, este problema sigue siendo considerado como un tema en la necesidad de un mayor estudio dentro de la comunidad ciencias de la tierra.
Esta investigación numérica parece arrojar al menos algo de luz sobre los cinco de estas cuestiones importantes. En primer lugar, en lo que se refiere a una fuente para el enorme volumen de fanerozoico sedimentos presentes en el registro de la roca continental, el estudio numérico revela que la erosión por cavitación tsunami impulsada durante el lapso de tiempo de la inundación puede generar nuevos sedimentos a una velocidad suficiente para dar cuenta de una fracción considerable del inventario de sedimentos Fanerozoico. La cavitación, que se producen a velocidades de agua de varias decenas de m / s, se reduce rápidamente cristalina rocas de la corteza continental de partículas de tamaño de arena y pequeñas.
Por otra parte, la existencia de tantas áreas escudo de hoy es testimonio de la realidad de la erosión extrema de la base ígnea sobre vastas porciones de los continentes de hoy en día. Estas áreas de escudo son extraordinariamente plana con poca o ninguna canalización de erosión y en general muestran poco o nada de deposición sedimentaria posterior a su intensa biselado de erosión. En el contexto de la inundación, estas zonas parecen ser candidatos obvios como las zonas de origen para al menos algunos de los sedimentos que encontramos en otras partes de la superficie continental. Una cuestión importante, sin embargo, es un mecanismo de erosión lo suficientemente potente como para erosionar tales roca cristalina dura a profundidades de hasta un kilómetro o más dentro de la duración de la inundación y también para hacerlo de una manera uniforme a través de dichas zonas lateralmente extensos. Los tsunamis, de gran amplitud frecuentes en este modelo numérico parecen ser adecuados para tal tarea. De hecho, es difícil imaginar un mecanismo alternativo capaz de llevar a cabo dicha erosión intensa y extensa lateralmente para producir una superficie con tan asombrosa planitud.
En lo que respecta a una explicación de por qué tanto los sedimentos se emplaza en la parte superior de los continentes cuando sus superficies en su mayoría se encuentran sobre el nivel del mar, este modelo numérico también proporciona una visión especialmente útil. La respuesta corta es que los tsunamis en un principio llevar más agua sobre la superficie de los continentes puede drenar por gravedad de nuevo en la cuenca del océano. Por lo tanto, el nivel del agua se eleva sobre la superficie de los continentes hasta la altura del agua es suficiente para que la tasa de escurrimiento para que coincida con la tasa de colocación de los tsunamis. Cabe destacar que, en los casos ilustrativos, la profundidad media del agua resultante es muchos cientos de metros, con valores máximos superiores a 1500 m (4921 pies) que se producen en los centros de giros anticiclónicos en las latitudes altas de ambos hemisferios norte y sur. Estos giros son expresiones de la fuerza de Coriolis causada por la rotación de la Tierra. Los giros sirven para organizar los movimientos generales de agua sobre las regiones continente en un patrón notablemente suave y coherente de flujo. Las velocidades de agua y profundidades son suficientes para mantener el nivel de turbulencia necesaria para suspender el tipo de gran volumen de sedimentos producidos por la erosión cavitación, para transportarlo a lugares distantes, ya que deposite que el sedimento en espesores de llegar a cientos de miles de metros sobre gran parte de la superficie continental. Las cuentas de flujos de tsunami impulsada no sólo por la erosión de importantes volúmenes de sedimentos, sino también su emplazamiento sobre el nivel del mar en la parte superior de los continentes en los patrones coherentes con grandes dimensiones laterales y espesores de más de un kilómetro.Así, el modelo parece explicar el emplazamiento del sedimento en la parte superior de la superficie continental y también para algunos aspectos de su carácter interno.
En lo que respecta al carácter interno de los depósitos sedimentarios sí mismos, el espacio horizontal de cerca de 120 kilómetros (74,5 millas) entre puntos de la rejilla en la rejilla de cálculo para este modelo global limita severamente el tipo de detalles estructurales que se pueden resolver a escala local dentro de capas de sedimentos individuales.Ciertamente hay evidencia observacional de los flujos de largo bajo el agua de salto de escombros, al parecer, impulsados por la gravedad, como la que generó la cama Whitmore Nautiloid en Arizona y Nevada. Tales observaciones han llamado la atención sobre la cuestión del mecanismo de transporte de sedimentos primaria durante la inundación, específicamente si el transporte fue principalmente por la gravedad impulsada por los flujos de escombros o sedimentos en suspensión en una espesa columna de agua en rápido movimiento turbulento. A pesar de que está más allá del alcance de lo que es factible para discutir aquí, los cálculos de este trabajo muestran que las concentraciones de sedimentos con frecuencia tienden a ser grandes, incluso hasta el punto de flujo hiper-concentrado en la base de la columna de agua turbulenta. En tales casos, parece que podría llegar a ser difícil de distinguir si el sedimento denso está siendo movido por gravedad o por medio de arrastre de arriba. Ciertamente, esta cuestión merece un estudio más detallado en el futuro.
Un resultado importante de esta investigación es que el mecanismo tsunami proporciona un sencillo de entender la explicación para el escurrimiento de las aguas de inundación de la superficie continental. A medida que la energía potencial gravitatoria del hundimiento placas litosféricas y el aumento de plumas del manto que había estado conduciendo los movimientos fuera de control comienzan a agotarse de manera significativa, las velocidades de la placa de la superficie comienzan a disminuir, los tsunamis empiezan a disminuir en frecuencia como en amplitud, los caudales de las corrientes de agua en los continentes comienzan a caer, y el agua que había sido emplazado y mantenido a lo largo de la superficie continental de tales grandes profundidades comienza a drenar nuevamente dentro de la cuenca del océano. El marco de tiempo de Génesis 8 indica que la escorrentía requiere unos cinco meses.De ahí que el modelo también se ocupa de las preguntas más comunes en cuanto a la fuente de las aguas de la inundación y donde estas aguas se fueron después de la inundación.
Los cálculos numéricos además proporcionan una posible explicación de los llamados cuencas sedimentarias. Como se ha mencionado en el Apéndice F, se encontró temprano en la probar el modelo que el sedimento espesores de varios cientos de metros rutinariamente surgir. Cuando se les permitió tan grandes espesores para aumentar la topografía continente original sin compensación isostática en absoluto, un tipo de inestabilidad numérica emergió. El comportamiento inestable implicó la formación de montículos localizadas de sedimentos, por lo general unos pocos cientos de kilómetros de diámetro y cientos de metros de altura. Esta topografía, a su vez, obligó al flujo de agua a concentrarse en los canales entre estos montículos de sedimento y para mejorar la deposición que se produzca en la parte superior de los montículos en las profundidades y velocidades de flujo eran pequeños. Cuanto mayores sean los montículos crecieron, más fuerte esta tendencia se hizo. Un remedio simple para este problema fue incluir la compensación isostática parcial para permitir el sótano a disminuir en respuesta a la carga de sedimentos por encima de ella. El esquema descrito en el Apéndice F alivia esta inestabilidad. Los montículos de sedimento, sin embargo, todavía surgen, pero con una amplitud reducida. Este comportamiento se observa en el modelo numérico sugiere una explicación simple y directo para la subsidencia asociada a lo que hoy se hace referencia a las cuencas sedimentarias como. La explicación es que los sedimentos que ahora se encuentran en los llamados cuencas corresponden a grandes pilas de sedimentos depositados en la superficie continental durante la inundación por los procesos de agua turbulentos a gran escala. El peso de estos montículos de sedimentos posteriormente ha deprimido la superficie original por debajo de los sedimentos en su actual perfil en forma de palangana.
Una característica notable de los resultados de cálculo es la profundidad significativa del agua en la mayor parte si no la mayoría de la superficie continental sostenido por tsunamis de gran amplitud frecuentes. Entre las cuestiones que esto plantea son observaciones tales como rastros de animales, los cuales indican algunas partes de la superficie de la tierra estaban por encima del agua. Es de destacar que en los casos ilustrativos después de unos 50 días la elevación topográfica de algunos de los montículos de sedimento les trae algunas de las veces por encima de la superficie del agua. Esto es consistente con el hecho de que evidencias de la exposición de la superficie de la tierra dentro de la parte del Paleozoico del registro sedimentario, es decir, durante la primera parte de la inundación, son escasos, mientras que tales evidencias se vuelven más y más común a través del Mesozoico y partes del Cenozoico de el registro, es decir, durante las últimas etapas de la inundación. Esta característica de altos niveles de agua en la mayor parte de la zona continental durante la mayor parte de la etapa de deposición de la inundación también tiene relación con la cuestión de dónde estaban siendo almacenadas y las plantas y animales enterrados en los sedimentos de las inundaciones posteriores durante las primeras etapas de la inundación. Los casos ilustrativos descritos en este documento parecen dar a entender que estaban ya sea flotando en la superficie del agua o estaban siendo persistentemente suspendidos por el flujo altamente turbulento. Otra posibilidad no se abordan en los casos ilustrativos, sin embargo, es que había regiones continentales-inundación pre con alta topografía que no se inundó hasta más tarde en la inundación. Los casos ilustrativos utilizan superficies lisas inicialmente continentales cuya máxima elevación sobre el nivel del mar nominal era de unos 100 m (328 pies). Es evidente que este tema merece un estudio más en el futuro.
Un aspecto crucial del modelo que también invita a un examen más detallado es el bloqueo / deslizamiento mecánica de la litosfera en subducción responsable en el modelo para la generación de los tsunamis de gran amplitud.velocidades de la placa durante la inundación, que está limitado por la escala de tiempo de Génesis capítulos 7 y 8 y las anchuras de nuevo suelo oceánico generado, debe haber habido al menos 108 veces más alta que es típico en la actualidad. Por otra parte, como se explica en el Apéndice F, la fuerza de roca del manto y posiblemente también gran parte de la litosfera se redujo por un factor similar. Por tanto, es difícil extrapolar con algún grado de confianza mecánica de la zona de subducción de hoy a la situación que prevaleció durante la inundación. En el mundo actual, la losa de subducción y la placa superior están siempre bloqueados, excepto por breves episodios que duran entre segundos y minutos, durante los cuales se produce un rápido deslizamiento, lo que resulta en grandes terremotos y tsunamis veces. El tiempo entre los eventos de deslizamiento en muchos segmentos de la zona de subducción de hoy se mide en términos de siglos. Una velocidad horizontal de 10 cm / año para una de las placas con la otra placa fija, por ejemplo, implica 10 m (32,8 pies) de deslizamiento entre las placas de cada 100 años o 20 m (65,6 pies) de deslizamiento cada 200 años. Cómo este proceso podría haber operado durante la inundación cuando la velocidad del plato eran mucho más altos está lejos de ser clara. La cuestión clave parece ser la cantidad de estrés la falla entre las placas podría sostener sin que se produzca deslizamiento. Es muy posible que la reducción de la resistencia debido al proceso fuera de control puede haber afectado a la litosfera inferior al manto debajo y permitió niveles relativamente altos de tensión en las placas bloqueadas y deflexiones superficiales en consecuencia más grandes entre los episodios de deslizamiento. Un estudio más cuidadoso, probablemente la utilización de herramientas numéricas, se necesita urgentemente para este tema vital.
Es de destacar que los dos casos ilustrativos presentados en este documento son muy simplista respecto a la Tierra real y todo el conjunto de procesos que jugó un papel durante la inundación. Una de las deficiencias más evidentes es que en ambos casos la configuración continente se mantuvo constante, sin ruptura continental y no posterior movimiento de los bloques componentes. Permitiendo la configuración inicial continente se rompa y los bloques resultantes de migrar casi con toda seguridad dará lugar a importantes cambios en los patrones de flujo de agua, la erosión y la sedimentación. Por otra parte, ninguno de los dos casos incluidos cualquier topografía inicial aparte de una superficie continente ligeramente abombado. Ni incluido cualquier topografía dinámica derivada de flujo de roca en el interior del manto. Tales variaciones en la altura de la superficie continente pueden alcanzar varios kilómetros de amplitud, especialmente cuando subducción se produce cerca de un margen continental.
Además, ni el cálculo incluido cualquier cambio en absoluto en el lugar o la actividad de las zonas de subducción. Los cambios temporales en donde se generan los tsunamis y su amplitud afectan, sin duda, los patrones de flujo de agua, la erosión y la sedimentación. Ninguno de los dos casos, incluidos los cambios temporales o espaciales en la altura del fondo del océano, ni cualquier sedimento fácilmente erosionables presente inicialmente en la superficie continental, ni ningún movimiento de los sedimentos depositados debido a deslizamientos de escombros por gravedad, ni ninguna contribución a la erosión del lecho de roca, desde la cosecha o la abrasión carga suspendida, ni cualquiera de una lista mucho más larga de procesos que, sin duda, han afectado a la distribución de los sedimentos de manera notable. En otras palabras, el modelo numérico se describe aquí no es más que un principio, un marco primitiva para tratar el flujo de agua, la erosión y la sedimentación de la inundación en una escala global. Es uno, sin embargo, que tiene la flexibilidad de ser aumentada para hacer frente a la mayoría de los problemas que acabamos de mencionar.
Sin embargo, incluso este marco comenzando está dando nuevas e importantes ideas. El hallazgo de que los tsunamis de gran amplitud producidas por el bloqueo y desbloqueo episódica de las placas de subducción del océano en el manto durante la inundación pueden causar profundidades significativas de agua de forma espontánea a acumularse sobre el interior del continente representa un descubrimiento notable. Uno de los mayores problemas no resueltos en relación con el diluvio del Génesis ha sido el mecanismo por el cual toda la superficie continental, posiblemente, podría ser inundado con agua. Una cuestión compañero ha sido el mecanismo responsable de la drenando de esta agua. La desaceleración constante de generación de tsunamis debido al agotamiento de la energía gravitacional conducir los movimientos de rocas en el manto durante las fases finales de la inundación hace que las velocidades del agua de manera constante a caer a cero y que el agua drene desde el continente. Ambos problemas se resuelven utilizando sólo el inventario de agua actualmente en las cuencas oceánicas del mundo. Estos mecanismos podrían posiblemente nunca han sido identificados, aparte de los experimentos de simulación numérica como éstas.
La versión de este modelo presentado en el 2013 Conferencia Internacional sobre Creacionismo (Baumgardner 2013) utiliza un mecanismo completamente diferente para conducir los movimientos de agua. En ese caso el mecanismo implicado varios enfoques cerca con la tierra de un cuerpo de tamaño de una luna que levantó mareas de gran amplitud. Ese documento sugiere que seis de tales encuentros cercanos espaciados unos 30 días de diferencia podrían plausiblemente dar cuenta de los seis megasecuencias tan prominente en el registro de los sedimentos y las discordancias erosivas casi globales asociados con ellos (Sloss 1963). En vista de los resultados presentados en este trabajo, cabe preguntarse si estos hallazgos más recientes sustituyen o incluso negar los anteriores. Es la opinión del autor de que los dos documentos y los dos mecanismos de forzamiento son compatibles entre sí. Para mí es al menos concebible que ambos mecanismos podrían haber operado durante la inundación. Sin embargo, el mecanismo de tsunami que se produce como consecuencia directa de las placas tectónicas rápidos que lógicamente debe haber tenido lugar durante la inundación-en mi opinión, es mucho más probable. Sobre todo porque el mecanismo de tsunami parece explicar tan fácilmente por la inundación de las regiones continentales durante la inundación y para la segunda vuelta en sus últimas etapas, creo que merece significativa mayor atención. El escenario de un enfoque de cerca con tierra por un organismo tamaño de la Luna se describe en el documento de 2013 fue, con toda franqueza, un esfuerzo de desesperación cerca de mi parte para identificar un mecanismo adecuado para conducir el flujo de agua.Si no fuera por la capacidad concebible de este escenario para dar cuenta de los megasecuencias, dudo que iba a tener un nivel suficiente de interés para perseguir seguir utilizándolo.
En el contexto de una defensa razonada de la inundación del Génesis, hay varias características principales de la superficie continental de la Tierra que reclaman una explicación. En primer lugar es el gran volumen de fosilíferos roca sedimentaria actualidad existen en la actualidad. El volumen es suficiente para cubrir la superficie continental a una profundidad media de aproximadamente 1.800 m o aproximadamente 1,1 mi. ¿Cuál fue el origen de este volumen masivo de sedimentos durante el corto lapso de tiempo de la inundación? En segundo lugar está la ubicación de este enorme volumen de sedimento. Se produce en la parte superior de los continentes, cuya superficie generalmente se encuentra por encima del nivel del mar. Esto plantea la pregunta, ¿qué tipo de proceso de agua podría concebiblemente emplazar tanto de sedimentos sobre el nivel del mar en la parte superior de la superficie de la tierra? Una tercera cuestión tiene que ver con los internos características de deposición de los sedimentos. En términos generales, la mayor parte de los sedimentos se produce como una sucesión vertical de capas horizontales, a menudo con gran extensión lateral. Tal esquema de capa-torta ordenada de los estratos lateralmente extensa se observa fácilmente, por ejemplo, por los sedimentos expuestos en las paredes del Gran Cañón. ¿Qué tipo de transporte y el proceso de deposición posiblemente podría generar tales capas uniformes sobre distancias tan grandes horizontales?
Una cuarta característica prominente de la superficie de la tierra incluye los llamados escudos continentales , incluyendo el canadiense, Báltico, Angaran (Siberia), África, India, Australia, y escudos de la Antártida. Estas grandes áreas de exposición ígneas y metamórficas del Precámbrico cristalina de alto grado rocas han experimentado una erosión significativa (a menudo con más de 1 km (0,62 millas) de roca cristalina eliminado), son casi plana, y tienen insignificante, en su caso, cubierta de sedimentos. ¿Cuándo en la historia de la tierra se produce tan intensa erosión si no fuera durante el Diluvio? Y por qué tipo de proceso?
Una quinta característica destacable es el fenómeno de las denominadas cuencas sedimentarias que cubren gran parte de las porciones no apantallado de la superficie de los continentes. Estas cuencas se describen comúnmente por la comunidad estándar de ciencias de la tierra como regiones de hundimiento a largo plazo que han proporcionado el espacio de alojamiento para el relleno con sedimentos. Frecuentes ausente de la discusión de la mayoría de las cuencas es el mecanismo responsable de su hundimiento. Sedimentos de cuenca, casi invariablemente, tienen sobre todo menores densidades que las rocas del basamento debajo. Dentro de interiores Cratón estables no hay ninguna razón obvia por la roca de densidad más baja en la superficie debe desplazar más alta densidad de la roca en la profundidad para producir hundimientos. Debido a un mecanismo convincente para el hundimiento no se ha producido en muchos contextos, este problema sigue siendo considerado como un tema en la necesidad de un mayor estudio dentro de la comunidad ciencias de la tierra.
Esta investigación numérica parece arrojar al menos algo de luz sobre los cinco de estas cuestiones importantes. En primer lugar, en lo que se refiere a una fuente para el enorme volumen de fanerozoico sedimentos presentes en el registro de la roca continental, el estudio numérico revela que la erosión por cavitación tsunami impulsada durante el lapso de tiempo de la inundación puede generar nuevos sedimentos a una velocidad suficiente para dar cuenta de una fracción considerable del inventario de sedimentos Fanerozoico. La cavitación, que se producen a velocidades de agua de varias decenas de m / s, se reduce rápidamente cristalina rocas de la corteza continental de partículas de tamaño de arena y pequeñas.
Por otra parte, la existencia de tantas áreas escudo de hoy es testimonio de la realidad de la erosión extrema de la base ígnea sobre vastas porciones de los continentes de hoy en día. Estas áreas de escudo son extraordinariamente plana con poca o ninguna canalización de erosión y en general muestran poco o nada de deposición sedimentaria posterior a su intensa biselado de erosión. En el contexto de la inundación, estas zonas parecen ser candidatos obvios como las zonas de origen para al menos algunos de los sedimentos que encontramos en otras partes de la superficie continental. Una cuestión importante, sin embargo, es un mecanismo de erosión lo suficientemente potente como para erosionar tales roca cristalina dura a profundidades de hasta un kilómetro o más dentro de la duración de la inundación y también para hacerlo de una manera uniforme a través de dichas zonas lateralmente extensos. Los tsunamis, de gran amplitud frecuentes en este modelo numérico parecen ser adecuados para tal tarea. De hecho, es difícil imaginar un mecanismo alternativo capaz de llevar a cabo dicha erosión intensa y extensa lateralmente para producir una superficie con tan asombrosa planitud.
En lo que respecta a una explicación de por qué tanto los sedimentos se emplaza en la parte superior de los continentes cuando sus superficies en su mayoría se encuentran sobre el nivel del mar, este modelo numérico también proporciona una visión especialmente útil. La respuesta corta es que los tsunamis en un principio llevar más agua sobre la superficie de los continentes puede drenar por gravedad de nuevo en la cuenca del océano. Por lo tanto, el nivel del agua se eleva sobre la superficie de los continentes hasta la altura del agua es suficiente para que la tasa de escurrimiento para que coincida con la tasa de colocación de los tsunamis. Cabe destacar que, en los casos ilustrativos, la profundidad media del agua resultante es muchos cientos de metros, con valores máximos superiores a 1500 m (4921 pies) que se producen en los centros de giros anticiclónicos en las latitudes altas de ambos hemisferios norte y sur. Estos giros son expresiones de la fuerza de Coriolis causada por la rotación de la Tierra. Los giros sirven para organizar los movimientos generales de agua sobre las regiones continente en un patrón notablemente suave y coherente de flujo. Las velocidades de agua y profundidades son suficientes para mantener el nivel de turbulencia necesaria para suspender el tipo de gran volumen de sedimentos producidos por la erosión cavitación, para transportarlo a lugares distantes, ya que deposite que el sedimento en espesores de llegar a cientos de miles de metros sobre gran parte de la superficie continental. Las cuentas de flujos de tsunami impulsada no sólo por la erosión de importantes volúmenes de sedimentos, sino también su emplazamiento sobre el nivel del mar en la parte superior de los continentes en los patrones coherentes con grandes dimensiones laterales y espesores de más de un kilómetro.Así, el modelo parece explicar el emplazamiento del sedimento en la parte superior de la superficie continental y también para algunos aspectos de su carácter interno.
En lo que respecta al carácter interno de los depósitos sedimentarios sí mismos, el espacio horizontal de cerca de 120 kilómetros (74,5 millas) entre puntos de la rejilla en la rejilla de cálculo para este modelo global limita severamente el tipo de detalles estructurales que se pueden resolver a escala local dentro de capas de sedimentos individuales.Ciertamente hay evidencia observacional de los flujos de largo bajo el agua de salto de escombros, al parecer, impulsados por la gravedad, como la que generó la cama Whitmore Nautiloid en Arizona y Nevada. Tales observaciones han llamado la atención sobre la cuestión del mecanismo de transporte de sedimentos primaria durante la inundación, específicamente si el transporte fue principalmente por la gravedad impulsada por los flujos de escombros o sedimentos en suspensión en una espesa columna de agua en rápido movimiento turbulento. A pesar de que está más allá del alcance de lo que es factible para discutir aquí, los cálculos de este trabajo muestran que las concentraciones de sedimentos con frecuencia tienden a ser grandes, incluso hasta el punto de flujo hiper-concentrado en la base de la columna de agua turbulenta. En tales casos, parece que podría llegar a ser difícil de distinguir si el sedimento denso está siendo movido por gravedad o por medio de arrastre de arriba. Ciertamente, esta cuestión merece un estudio más detallado en el futuro.
Un resultado importante de esta investigación es que el mecanismo tsunami proporciona un sencillo de entender la explicación para el escurrimiento de las aguas de inundación de la superficie continental. A medida que la energía potencial gravitatoria del hundimiento placas litosféricas y el aumento de plumas del manto que había estado conduciendo los movimientos fuera de control comienzan a agotarse de manera significativa, las velocidades de la placa de la superficie comienzan a disminuir, los tsunamis empiezan a disminuir en frecuencia como en amplitud, los caudales de las corrientes de agua en los continentes comienzan a caer, y el agua que había sido emplazado y mantenido a lo largo de la superficie continental de tales grandes profundidades comienza a drenar nuevamente dentro de la cuenca del océano. El marco de tiempo de Génesis 8 indica que la escorrentía requiere unos cinco meses.De ahí que el modelo también se ocupa de las preguntas más comunes en cuanto a la fuente de las aguas de la inundación y donde estas aguas se fueron después de la inundación.
Los cálculos numéricos además proporcionan una posible explicación de los llamados cuencas sedimentarias. Como se ha mencionado en el Apéndice F, se encontró temprano en la probar el modelo que el sedimento espesores de varios cientos de metros rutinariamente surgir. Cuando se les permitió tan grandes espesores para aumentar la topografía continente original sin compensación isostática en absoluto, un tipo de inestabilidad numérica emergió. El comportamiento inestable implicó la formación de montículos localizadas de sedimentos, por lo general unos pocos cientos de kilómetros de diámetro y cientos de metros de altura. Esta topografía, a su vez, obligó al flujo de agua a concentrarse en los canales entre estos montículos de sedimento y para mejorar la deposición que se produzca en la parte superior de los montículos en las profundidades y velocidades de flujo eran pequeños. Cuanto mayores sean los montículos crecieron, más fuerte esta tendencia se hizo. Un remedio simple para este problema fue incluir la compensación isostática parcial para permitir el sótano a disminuir en respuesta a la carga de sedimentos por encima de ella. El esquema descrito en el Apéndice F alivia esta inestabilidad. Los montículos de sedimento, sin embargo, todavía surgen, pero con una amplitud reducida. Este comportamiento se observa en el modelo numérico sugiere una explicación simple y directo para la subsidencia asociada a lo que hoy se hace referencia a las cuencas sedimentarias como. La explicación es que los sedimentos que ahora se encuentran en los llamados cuencas corresponden a grandes pilas de sedimentos depositados en la superficie continental durante la inundación por los procesos de agua turbulentos a gran escala. El peso de estos montículos de sedimentos posteriormente ha deprimido la superficie original por debajo de los sedimentos en su actual perfil en forma de palangana.
Una característica notable de los resultados de cálculo es la profundidad significativa del agua en la mayor parte si no la mayoría de la superficie continental sostenido por tsunamis de gran amplitud frecuentes. Entre las cuestiones que esto plantea son observaciones tales como rastros de animales, los cuales indican algunas partes de la superficie de la tierra estaban por encima del agua. Es de destacar que en los casos ilustrativos después de unos 50 días la elevación topográfica de algunos de los montículos de sedimento les trae algunas de las veces por encima de la superficie del agua. Esto es consistente con el hecho de que evidencias de la exposición de la superficie de la tierra dentro de la parte del Paleozoico del registro sedimentario, es decir, durante la primera parte de la inundación, son escasos, mientras que tales evidencias se vuelven más y más común a través del Mesozoico y partes del Cenozoico de el registro, es decir, durante las últimas etapas de la inundación. Esta característica de altos niveles de agua en la mayor parte de la zona continental durante la mayor parte de la etapa de deposición de la inundación también tiene relación con la cuestión de dónde estaban siendo almacenadas y las plantas y animales enterrados en los sedimentos de las inundaciones posteriores durante las primeras etapas de la inundación. Los casos ilustrativos descritos en este documento parecen dar a entender que estaban ya sea flotando en la superficie del agua o estaban siendo persistentemente suspendidos por el flujo altamente turbulento. Otra posibilidad no se abordan en los casos ilustrativos, sin embargo, es que había regiones continentales-inundación pre con alta topografía que no se inundó hasta más tarde en la inundación. Los casos ilustrativos utilizan superficies lisas inicialmente continentales cuya máxima elevación sobre el nivel del mar nominal era de unos 100 m (328 pies). Es evidente que este tema merece un estudio más en el futuro.
Un aspecto crucial del modelo que también invita a un examen más detallado es el bloqueo / deslizamiento mecánica de la litosfera en subducción responsable en el modelo para la generación de los tsunamis de gran amplitud.velocidades de la placa durante la inundación, que está limitado por la escala de tiempo de Génesis capítulos 7 y 8 y las anchuras de nuevo suelo oceánico generado, debe haber habido al menos 108 veces más alta que es típico en la actualidad. Por otra parte, como se explica en el Apéndice F, la fuerza de roca del manto y posiblemente también gran parte de la litosfera se redujo por un factor similar. Por tanto, es difícil extrapolar con algún grado de confianza mecánica de la zona de subducción de hoy a la situación que prevaleció durante la inundación. En el mundo actual, la losa de subducción y la placa superior están siempre bloqueados, excepto por breves episodios que duran entre segundos y minutos, durante los cuales se produce un rápido deslizamiento, lo que resulta en grandes terremotos y tsunamis veces. El tiempo entre los eventos de deslizamiento en muchos segmentos de la zona de subducción de hoy se mide en términos de siglos. Una velocidad horizontal de 10 cm / año para una de las placas con la otra placa fija, por ejemplo, implica 10 m (32,8 pies) de deslizamiento entre las placas de cada 100 años o 20 m (65,6 pies) de deslizamiento cada 200 años. Cómo este proceso podría haber operado durante la inundación cuando la velocidad del plato eran mucho más altos está lejos de ser clara. La cuestión clave parece ser la cantidad de estrés la falla entre las placas podría sostener sin que se produzca deslizamiento. Es muy posible que la reducción de la resistencia debido al proceso fuera de control puede haber afectado a la litosfera inferior al manto debajo y permitió niveles relativamente altos de tensión en las placas bloqueadas y deflexiones superficiales en consecuencia más grandes entre los episodios de deslizamiento. Un estudio más cuidadoso, probablemente la utilización de herramientas numéricas, se necesita urgentemente para este tema vital.
Es de destacar que los dos casos ilustrativos presentados en este documento son muy simplista respecto a la Tierra real y todo el conjunto de procesos que jugó un papel durante la inundación. Una de las deficiencias más evidentes es que en ambos casos la configuración continente se mantuvo constante, sin ruptura continental y no posterior movimiento de los bloques componentes. Permitiendo la configuración inicial continente se rompa y los bloques resultantes de migrar casi con toda seguridad dará lugar a importantes cambios en los patrones de flujo de agua, la erosión y la sedimentación. Por otra parte, ninguno de los dos casos incluidos cualquier topografía inicial aparte de una superficie continente ligeramente abombado. Ni incluido cualquier topografía dinámica derivada de flujo de roca en el interior del manto. Tales variaciones en la altura de la superficie continente pueden alcanzar varios kilómetros de amplitud, especialmente cuando subducción se produce cerca de un margen continental.
Además, ni el cálculo incluido cualquier cambio en absoluto en el lugar o la actividad de las zonas de subducción. Los cambios temporales en donde se generan los tsunamis y su amplitud afectan, sin duda, los patrones de flujo de agua, la erosión y la sedimentación. Ninguno de los dos casos, incluidos los cambios temporales o espaciales en la altura del fondo del océano, ni cualquier sedimento fácilmente erosionables presente inicialmente en la superficie continental, ni ningún movimiento de los sedimentos depositados debido a deslizamientos de escombros por gravedad, ni ninguna contribución a la erosión del lecho de roca, desde la cosecha o la abrasión carga suspendida, ni cualquiera de una lista mucho más larga de procesos que, sin duda, han afectado a la distribución de los sedimentos de manera notable. En otras palabras, el modelo numérico se describe aquí no es más que un principio, un marco primitiva para tratar el flujo de agua, la erosión y la sedimentación de la inundación en una escala global. Es uno, sin embargo, que tiene la flexibilidad de ser aumentada para hacer frente a la mayoría de los problemas que acabamos de mencionar.
Sin embargo, incluso este marco comenzando está dando nuevas e importantes ideas. El hallazgo de que los tsunamis de gran amplitud producidas por el bloqueo y desbloqueo episódica de las placas de subducción del océano en el manto durante la inundación pueden causar profundidades significativas de agua de forma espontánea a acumularse sobre el interior del continente representa un descubrimiento notable. Uno de los mayores problemas no resueltos en relación con el diluvio del Génesis ha sido el mecanismo por el cual toda la superficie continental, posiblemente, podría ser inundado con agua. Una cuestión compañero ha sido el mecanismo responsable de la drenando de esta agua. La desaceleración constante de generación de tsunamis debido al agotamiento de la energía gravitacional conducir los movimientos de rocas en el manto durante las fases finales de la inundación hace que las velocidades del agua de manera constante a caer a cero y que el agua drene desde el continente. Ambos problemas se resuelven utilizando sólo el inventario de agua actualmente en las cuencas oceánicas del mundo. Estos mecanismos podrían posiblemente nunca han sido identificados, aparte de los experimentos de simulación numérica como éstas.
La versión de este modelo presentado en el 2013 Conferencia Internacional sobre Creacionismo (Baumgardner 2013) utiliza un mecanismo completamente diferente para conducir los movimientos de agua. En ese caso el mecanismo implicado varios enfoques cerca con la tierra de un cuerpo de tamaño de una luna que levantó mareas de gran amplitud. Ese documento sugiere que seis de tales encuentros cercanos espaciados unos 30 días de diferencia podrían plausiblemente dar cuenta de los seis megasecuencias tan prominente en el registro de los sedimentos y las discordancias erosivas casi globales asociados con ellos (Sloss 1963). En vista de los resultados presentados en este trabajo, cabe preguntarse si estos hallazgos más recientes sustituyen o incluso negar los anteriores. Es la opinión del autor de que los dos documentos y los dos mecanismos de forzamiento son compatibles entre sí. Para mí es al menos concebible que ambos mecanismos podrían haber operado durante la inundación. Sin embargo, el mecanismo de tsunami que se produce como consecuencia directa de las placas tectónicas rápidos que lógicamente debe haber tenido lugar durante la inundación-en mi opinión, es mucho más probable. Sobre todo porque el mecanismo de tsunami parece explicar tan fácilmente por la inundación de las regiones continentales durante la inundación y para la segunda vuelta en sus últimas etapas, creo que merece significativa mayor atención. El escenario de un enfoque de cerca con tierra por un organismo tamaño de la Luna se describe en el documento de 2013 fue, con toda franqueza, un esfuerzo de desesperación cerca de mi parte para identificar un mecanismo adecuado para conducir el flujo de agua.Si no fuera por la capacidad concebible de este escenario para dar cuenta de los megasecuencias, dudo que iba a tener un nivel suficiente de interés para perseguir seguir utilizándolo.
Conclusión
Simulación numérica ofrece un medio para la investigación de los fenómenos que son imposibles, ya sea debido a su escala física o las condiciones extremas que conllevan, o ambos, para explorar experimentalmente de manera repetible en el laboratorio. El Diluvio del Génesis, sin duda entra en esta categoría. En este trabajo se describe un intento de comenzar a aplicar las leyes físicas conocidas, los procesos físicos que pueden ser investigados en el laboratorio, y los procesos a escalas mayores que pueden ser estudiadas y caracterizadas por mediciones en el presente, para modelar aspectos importantes de este acontecimiento catastrófico único. El modelo numérico explota la aproximación aguas poco profundas para representar el flujo de agua en una capa fina sobre la superficie de una esfera en rotación que corresponde a la tierra. Se utiliza la teoría de flujo en canales abiertos para el tratamiento de la suspensión y el transporte de sedimentos por el agua que fluye turbulento. Como su mecanismo de erosión que utiliza la cavitación. Para conducir el flujo de agua que se basa en consecuencia actualmente observable de la tectónica de placas, es decir, el bloqueo y la liberación repentina de una placa litosférica subducting lo largo de su contacto de fallo con la placa superior en una zona de subducción. Hoy en día, cuando una placa de subducción desbloquea y rebotes, el movimiento hacia arriba de la placa pueden, ya menudo lo hace, generar una onda de agua conocido como un tsunami.Durante la inundación, cuando la velocidad del plato eran órdenes de magnitud mayor que en la actualidad, las amplitudes de los tsunamis concebible que pueden haber sido mucho más grande.
En el modelo numérico tales tsunamis de gran amplitud conducen el flujo global del agua. Estos tsunamis, sorprendentemente, inundan las regiones continentales de todo el mundo con muchos cientos de metros de agua. Los tsunamis inicialmente emplace agua en el continente más rápido de lo que puede salir corriendo bajo la influencia de la gravedad. El equilibrio entre el emplazamiento de agua y aguas de escorrentía se produce sólo después de que el agua sobre la superficie continental alcanza profundidades de varios cientos de metros. Mientras tanto, las velocidades del agua a lo largo de los márgenes continentales superan rápidamente el umbral de cavitación, lo que lleva a una intensa erosión de la roca madre no continental. El efecto de Coriolis causada por la rotación de la tierra conduce a patrones grandes, en su mayoría fijos, la circulación a altas latitudes superiores a las regiones continentales de ambos hemisferios norte y sur. El flujo a gran escala de la persistencia de agua turbulenta transporta el sedimento erosionado y lo deposita en un patrón caracterizado por grandes escalas espaciales. Cuando las velocidades de placas comienzan a caer debido al agotamiento de la energía gravitacional conducir el movimiento en el manto, la disminución tsunamis en frecuencia y en amplitud, velocidad del agua caen hacia cero, y el agua que había estado de pie cientos de metros de profundidad sobre la superficie continental drena de nuevo en la cuenca del océano. En los dos ejemplos ilustrativos, las tasas de erosión y deposición se acercan a los necesarios para dar cuenta de la 1800 m (5905 pies) de sedimento en promedio que las mantas superficie continental de hoy.
Este modelo numérico, ya que es básico, arroja nueva luz sobre varias cuestiones importantes relacionadas con la inundación. Parece para tener en cuenta (1) de cómo los continentes, que hoy en día son en su mayoría sobre el nivel del mar, estaban profundamente inundados durante la inundación; (2) para la fuente del agua responsable de la inundación; y (3) de donde todo lo que el agua se fue al final de la inundación. Al parecer, para tener en cuenta (4) para ver cómo podría surgir un gran volumen de nuevos sedimentos tales durante el corto lapso de tiempo de la inundación; (5) para ver cómo las secuencias de sedimentos gruesos asombrosamente que observamos en el registro sedimentario lograron ser depositado en la parte superior de los continentes normalmente de alto standing; y (6) para la gran escamas laterales y continuidad horizontal de muchos, si no la mayoría de las capas individuales dentro de la secuencia de sedimentos. Al parecer, para tener en cuenta (7) para las vastas regiones, roca basamento precámbrico profundamente biselada plana conocidos como escudos continentales. Por último, es muy posible que la cuenta (8) para la que se encuentra detrás cuencas sedimentarias.
Estos resultados prometedores invitan varias mejoras y adiciones futuras. Los ejemplos incluyen aumentar el modelo para el tratamiento de la fractura continental, movimientos de los bloques continentales resultantes, la migración de las zonas de subducción, y la topografía dinámica del movimiento ascendente de la roca en el interior del manto. Tales refinamientos casi con toda seguridad dará lugar a percepciones adicionales con respecto a este cataclismo que en los días de Noé alteró dramáticamente la faz de la tierra. Mi oración es que una mejor comprensión de los procesos que genera el registro de sedimentos fosilíferos durante la inundación podría fortalecer la confianza de muchos en la fiabilidad histórica de Génesis 1-11 , y por lo tanto su confianza en la totalidad de la Escritura, y de este modo fortalecer su lealtad y devoción al Señor Jesús.
Simulación numérica ofrece un medio para la investigación de los fenómenos que son imposibles, ya sea debido a su escala física o las condiciones extremas que conllevan, o ambos, para explorar experimentalmente de manera repetible en el laboratorio. El Diluvio del Génesis, sin duda entra en esta categoría. En este trabajo se describe un intento de comenzar a aplicar las leyes físicas conocidas, los procesos físicos que pueden ser investigados en el laboratorio, y los procesos a escalas mayores que pueden ser estudiadas y caracterizadas por mediciones en el presente, para modelar aspectos importantes de este acontecimiento catastrófico único. El modelo numérico explota la aproximación aguas poco profundas para representar el flujo de agua en una capa fina sobre la superficie de una esfera en rotación que corresponde a la tierra. Se utiliza la teoría de flujo en canales abiertos para el tratamiento de la suspensión y el transporte de sedimentos por el agua que fluye turbulento. Como su mecanismo de erosión que utiliza la cavitación. Para conducir el flujo de agua que se basa en consecuencia actualmente observable de la tectónica de placas, es decir, el bloqueo y la liberación repentina de una placa litosférica subducting lo largo de su contacto de fallo con la placa superior en una zona de subducción. Hoy en día, cuando una placa de subducción desbloquea y rebotes, el movimiento hacia arriba de la placa pueden, ya menudo lo hace, generar una onda de agua conocido como un tsunami.Durante la inundación, cuando la velocidad del plato eran órdenes de magnitud mayor que en la actualidad, las amplitudes de los tsunamis concebible que pueden haber sido mucho más grande.
En el modelo numérico tales tsunamis de gran amplitud conducen el flujo global del agua. Estos tsunamis, sorprendentemente, inundan las regiones continentales de todo el mundo con muchos cientos de metros de agua. Los tsunamis inicialmente emplace agua en el continente más rápido de lo que puede salir corriendo bajo la influencia de la gravedad. El equilibrio entre el emplazamiento de agua y aguas de escorrentía se produce sólo después de que el agua sobre la superficie continental alcanza profundidades de varios cientos de metros. Mientras tanto, las velocidades del agua a lo largo de los márgenes continentales superan rápidamente el umbral de cavitación, lo que lleva a una intensa erosión de la roca madre no continental. El efecto de Coriolis causada por la rotación de la tierra conduce a patrones grandes, en su mayoría fijos, la circulación a altas latitudes superiores a las regiones continentales de ambos hemisferios norte y sur. El flujo a gran escala de la persistencia de agua turbulenta transporta el sedimento erosionado y lo deposita en un patrón caracterizado por grandes escalas espaciales. Cuando las velocidades de placas comienzan a caer debido al agotamiento de la energía gravitacional conducir el movimiento en el manto, la disminución tsunamis en frecuencia y en amplitud, velocidad del agua caen hacia cero, y el agua que había estado de pie cientos de metros de profundidad sobre la superficie continental drena de nuevo en la cuenca del océano. En los dos ejemplos ilustrativos, las tasas de erosión y deposición se acercan a los necesarios para dar cuenta de la 1800 m (5905 pies) de sedimento en promedio que las mantas superficie continental de hoy.
Este modelo numérico, ya que es básico, arroja nueva luz sobre varias cuestiones importantes relacionadas con la inundación. Parece para tener en cuenta (1) de cómo los continentes, que hoy en día son en su mayoría sobre el nivel del mar, estaban profundamente inundados durante la inundación; (2) para la fuente del agua responsable de la inundación; y (3) de donde todo lo que el agua se fue al final de la inundación. Al parecer, para tener en cuenta (4) para ver cómo podría surgir un gran volumen de nuevos sedimentos tales durante el corto lapso de tiempo de la inundación; (5) para ver cómo las secuencias de sedimentos gruesos asombrosamente que observamos en el registro sedimentario lograron ser depositado en la parte superior de los continentes normalmente de alto standing; y (6) para la gran escamas laterales y continuidad horizontal de muchos, si no la mayoría de las capas individuales dentro de la secuencia de sedimentos. Al parecer, para tener en cuenta (7) para las vastas regiones, roca basamento precámbrico profundamente biselada plana conocidos como escudos continentales. Por último, es muy posible que la cuenta (8) para la que se encuentra detrás cuencas sedimentarias.
Estos resultados prometedores invitan varias mejoras y adiciones futuras. Los ejemplos incluyen aumentar el modelo para el tratamiento de la fractura continental, movimientos de los bloques continentales resultantes, la migración de las zonas de subducción, y la topografía dinámica del movimiento ascendente de la roca en el interior del manto. Tales refinamientos casi con toda seguridad dará lugar a percepciones adicionales con respecto a este cataclismo que en los días de Noé alteró dramáticamente la faz de la tierra. Mi oración es que una mejor comprensión de los procesos que genera el registro de sedimentos fosilíferos durante la inundación podría fortalecer la confianza de muchos en la fiabilidad histórica de Génesis 1-11 , y por lo tanto su confianza en la totalidad de la Escritura, y de este modo fortalecer su lealtad y devoción al Señor Jesús.
Referencias
Ager, DV 1973. La naturaleza del registro estratigráfico . Londres, Reino Unido: MacMillan.
Apsley, DD 2009. "Estructura de una capa turbulenta de Límites" (notas de la conferencia del curso titulado "Capas límite turbulenta," la Universidad de Manchester, Reino Unido). http: // personalpages.manchester.ac.uk/staff/david.d.apsley/ conferencias / turbbl / regions.pdf.
Arndt, REA 1981. "La cavitación en las máquinas de fluidos y estructuras hidráulicas." Annual Reviews de Mecánica de Fluidos 13: 273-328.
Austin, SA ed. 1994. Gran Cañón: Monumento a la catástrofe . Santee, California: Instituto para la Investigación de la Creación.
Bagnold, RA 1966. "Una aproximación al problema del transporte de sedimentos de Física General." Geological Survey Papel Profesional 422-I, I1-I37. Washington, DC: Oficina de Impresión del Gobierno de los Estados Unidos.
Baker, V. 1974. "Formas de erosión y procesos de las catastróficas inundaciones del Pleistoceno Missoula en el este de Washington." En fluvial Geomorfología . Editado por M. Morisawa, 123-48. Londres, Reino Unido: Allen y Unwin.
Baumgardner, JR 2013. "Al explicar la fósiles Continental Teniendo sedimentos récord en términos de diluvio del Génesis: Insights de Modelación Numérica de erosión, transporte de sedimentos y procesos de deposición en una escala global." En las Actas de la Séptima Conferencia Internacional sobre Creacionismo . Editado por M. Horstemeyer.Pittsburgh, Pennsylvania: Ciencia de la Creación Fellowship, Inc. http: // media.wix.com/ugd/a704d4_70de439475d229ba9231b545d e57d670.pdf.
Baumgardner, JR 2003. "Tectónica de placas catastrófica: La física detrás del diluvio del Génesis." En Actas de la Quinta Conferencia Internacional sobre Creacionismo . Editado por RL Ivey Jr., 113-26. Pittsburgh, Pennsylvania: Ciencia de la Creación de becas. http://media.wix.com/ugd/a704d4_ bfc60d3bb5aad292ce1e8d9384b9eb87.pdf.
Chanson, H. 1997. burbuja de aire en el arrastre libre en superficie turbulenta de cizallamiento flujos . Londres, Reino Unido: Academic Press.
Darcy, H. 1857. Los familiares Investigaciones Experimentales Au Mouvement de l'Eau dans les Tuyaux (Experimental Research En relación con el movimiento del agua en tuberías) . París, Francia: Mallet-Bachelier.
Falvey, HT 1990. "La cavitación de las mangas y vertederos." Ingeniería Monografía No. 42. Denver, Colorado: US Bureau of Reclamation.
. Hagen, G. 1854. "Über den Einfluss der Temperatura auf die Bewegung des Wassers en Röhren" ( "Sobre la influencia de la temperatura sobre el movimiento del agua en tuberías") Mathematische Abhandlungen der Akademie der Wissenschaften Koeniglichen zu Berlin : 17-98 .
Harris, CK 2003. "suspendido el transporte de sedimentos" (notas de la conferencia de curso de postgrado titulado "Procesos de transporte de sedimentos en Ambientes Costeros," Virginia Instituto de Ciencias del Mar).http://www.vims.edu/~ckharris/ MS698_03 / lecture_08.pdf.
Jiménez, J., y O. Madsen. 2003. "Una fórmula simple para estimar la velocidad de sedimentación de los sedimentos naturales." Diario de canal, puerto, Costa, e Ingeniería Oceánica 129 (2): 70-78.
Kolmogorov, AN (1941) 1991a. "La estructura local de la turbulencia en los fluidos viscosos incompresibles en números muy grandes de Reynolds." Doklady Akademii Nauk SSSR 30: 299-303. Reproducido en Actas de la Royal Society de Londres , serie A, 434: 9-13.
Kolmogorov, AN (1941) 1991b. "La disipación de energía en el nivel local turbulencia isotrópica." Doklady Akademii Nauk SSSR 32: 19-21. Reproducido en Actas: Ciencias Matemáticas y Físicas 434 (1890): 15-17.
Majewski, D., D. Liermann, P. Prohl, B. Ritter, M. Buchhold, T. Hanisch, G. Paul, W. Wergen, y J. Baumgardner. 2002. "The Global Icosahedral-hexagonal GridPoint Modelo GME:. Descripción y Análisis de alta resolución" Monthly Weather Review 130 (2): 319-38.
Momber, AW 2003. "El daño a la cavitación Geomateriales en un sistema que fluye." Revista de Ciencia de los Materiales 38 (4): 747-57.
Murai, H., S. Nishi, S. Shimizu, Y. Murakami, Y. Hara, T. Kuroda, y S. Yaguchi. 1997. "La dependencia de la velocidad de cavitación daños (Hoja-Tipo cavitación)." Transacciones de la Sociedad Japonesa de Ingenieros Mecánicos , Parte B 63 (607): 750-56.
O'Connor, JE 1993. "Hidrología, Hidráulica y Geomorfología de la Bonneville inundación." Geological Society of America Papel especial 274.
Papa, SB 2000. turbulento flujos . Cambridge, Reino Unido: Cambridge University Press.
Prandtl, L. 1905. "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" ( "El flujo de fluido con muy poca fricción").Verhandlungen des Dritten internationalen mathematischen Kongresses , Heidelberg, 484-91. Leipzig, Alemania: Teubner Verlag.
Prothero, DR, y F. Schwab. 2004. Geología Sedimentaria: Una introducción a las rocas sedimentarias y estratigrafía . 2ª ed.Nueva York, Nueva York: WH Freeman.
Reynolds, O. 1883. "Una Investigación Experimental de las circunstancias que determinan si el movimiento del agua será directa o sinuoso, y de la Ley de la Resistencia en canales paralelos." Philosophical Transactions de la Royal Society de Londres 174: 935-82 .
Richardson, LF 1920. "El suministro de energía desde y hacia remolinos atmosféricos." Proceedings of the Royal Society de Londres, serie A , 97 (686): 354-37.
Sloss, LL 1963. "Secuencias en la cratónica interior de América del Norte." Sociedad Geológica de América Boletín 74 (2): 93-113.
Staniforth, A. y J. Côté. 1991. "Esquemas de Integración semi-de Lagrange para los modelos atmosféricos-A Review."Monthly Weather Review 119: 2206-223.
Stokes, G. 1851. "sobre el efecto de la fricción interna de los fluidos en el movimiento de los péndulos." Transacciones de la Sociedad Filosófica de Cambridge 9: 8-106.
Whipple, KX, GS Hancock, y RS Anderson. 2000. "Río incisión en la roca: Mecánica y eficacia relativa de desplume, a la abrasión y cavitación." Geological Society of America Bulletin 112 (1-2): 490-503.
Williamson, DL, JB Drake, JJ Hack, R. Jakob, y PN Swaztrauber. 1992. "Una prueba estándar establecido para numéricas Aproximaciones a las ecuaciones de aguas someras en Geometría esférica." Journal of Computational Physics 102 (1): 211-24.
Winston, D., y PK Enlace, 1993. "Rocas de Medio proterozoicas de Montana, Idaho y Washington: El Cinturón supergrupo." En Precámbrico de la Estados Unidos contiguos . Editado por J. Reed, P. Simms, R. Houston, D. Rankin, P. Link, R. Van Schmus, y P. Bickford, 487-521. Boulder, Colorado: v. Geological Society of America, la geología de América del Norte, C-3.
Wohl, EE 1992. "Bancos roca de fondo y Bares: Boulder. Las inundaciones en el Burdekin Garganta de Australia"Geological Society of America Bulletin 104 (6): 770-78.
Ager, DV 1973. La naturaleza del registro estratigráfico . Londres, Reino Unido: MacMillan.
Apsley, DD 2009. "Estructura de una capa turbulenta de Límites" (notas de la conferencia del curso titulado "Capas límite turbulenta," la Universidad de Manchester, Reino Unido). http: // personalpages.manchester.ac.uk/staff/david.d.apsley/ conferencias / turbbl / regions.pdf.
Arndt, REA 1981. "La cavitación en las máquinas de fluidos y estructuras hidráulicas." Annual Reviews de Mecánica de Fluidos 13: 273-328.
Austin, SA ed. 1994. Gran Cañón: Monumento a la catástrofe . Santee, California: Instituto para la Investigación de la Creación.
Bagnold, RA 1966. "Una aproximación al problema del transporte de sedimentos de Física General." Geological Survey Papel Profesional 422-I, I1-I37. Washington, DC: Oficina de Impresión del Gobierno de los Estados Unidos.
Baker, V. 1974. "Formas de erosión y procesos de las catastróficas inundaciones del Pleistoceno Missoula en el este de Washington." En fluvial Geomorfología . Editado por M. Morisawa, 123-48. Londres, Reino Unido: Allen y Unwin.
Baumgardner, JR 2013. "Al explicar la fósiles Continental Teniendo sedimentos récord en términos de diluvio del Génesis: Insights de Modelación Numérica de erosión, transporte de sedimentos y procesos de deposición en una escala global." En las Actas de la Séptima Conferencia Internacional sobre Creacionismo . Editado por M. Horstemeyer.Pittsburgh, Pennsylvania: Ciencia de la Creación Fellowship, Inc. http: // media.wix.com/ugd/a704d4_70de439475d229ba9231b545d e57d670.pdf.
Baumgardner, JR 2003. "Tectónica de placas catastrófica: La física detrás del diluvio del Génesis." En Actas de la Quinta Conferencia Internacional sobre Creacionismo . Editado por RL Ivey Jr., 113-26. Pittsburgh, Pennsylvania: Ciencia de la Creación de becas. http://media.wix.com/ugd/a704d4_ bfc60d3bb5aad292ce1e8d9384b9eb87.pdf.
Chanson, H. 1997. burbuja de aire en el arrastre libre en superficie turbulenta de cizallamiento flujos . Londres, Reino Unido: Academic Press.
Darcy, H. 1857. Los familiares Investigaciones Experimentales Au Mouvement de l'Eau dans les Tuyaux (Experimental Research En relación con el movimiento del agua en tuberías) . París, Francia: Mallet-Bachelier.
Falvey, HT 1990. "La cavitación de las mangas y vertederos." Ingeniería Monografía No. 42. Denver, Colorado: US Bureau of Reclamation.
. Hagen, G. 1854. "Über den Einfluss der Temperatura auf die Bewegung des Wassers en Röhren" ( "Sobre la influencia de la temperatura sobre el movimiento del agua en tuberías") Mathematische Abhandlungen der Akademie der Wissenschaften Koeniglichen zu Berlin : 17-98 .
Harris, CK 2003. "suspendido el transporte de sedimentos" (notas de la conferencia de curso de postgrado titulado "Procesos de transporte de sedimentos en Ambientes Costeros," Virginia Instituto de Ciencias del Mar).http://www.vims.edu/~ckharris/ MS698_03 / lecture_08.pdf.
Jiménez, J., y O. Madsen. 2003. "Una fórmula simple para estimar la velocidad de sedimentación de los sedimentos naturales." Diario de canal, puerto, Costa, e Ingeniería Oceánica 129 (2): 70-78.
Kolmogorov, AN (1941) 1991a. "La estructura local de la turbulencia en los fluidos viscosos incompresibles en números muy grandes de Reynolds." Doklady Akademii Nauk SSSR 30: 299-303. Reproducido en Actas de la Royal Society de Londres , serie A, 434: 9-13.
Kolmogorov, AN (1941) 1991b. "La disipación de energía en el nivel local turbulencia isotrópica." Doklady Akademii Nauk SSSR 32: 19-21. Reproducido en Actas: Ciencias Matemáticas y Físicas 434 (1890): 15-17.
Majewski, D., D. Liermann, P. Prohl, B. Ritter, M. Buchhold, T. Hanisch, G. Paul, W. Wergen, y J. Baumgardner. 2002. "The Global Icosahedral-hexagonal GridPoint Modelo GME:. Descripción y Análisis de alta resolución" Monthly Weather Review 130 (2): 319-38.
Momber, AW 2003. "El daño a la cavitación Geomateriales en un sistema que fluye." Revista de Ciencia de los Materiales 38 (4): 747-57.
Murai, H., S. Nishi, S. Shimizu, Y. Murakami, Y. Hara, T. Kuroda, y S. Yaguchi. 1997. "La dependencia de la velocidad de cavitación daños (Hoja-Tipo cavitación)." Transacciones de la Sociedad Japonesa de Ingenieros Mecánicos , Parte B 63 (607): 750-56.
O'Connor, JE 1993. "Hidrología, Hidráulica y Geomorfología de la Bonneville inundación." Geological Society of America Papel especial 274.
Papa, SB 2000. turbulento flujos . Cambridge, Reino Unido: Cambridge University Press.
Prandtl, L. 1905. "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" ( "El flujo de fluido con muy poca fricción").Verhandlungen des Dritten internationalen mathematischen Kongresses , Heidelberg, 484-91. Leipzig, Alemania: Teubner Verlag.
Prothero, DR, y F. Schwab. 2004. Geología Sedimentaria: Una introducción a las rocas sedimentarias y estratigrafía . 2ª ed.Nueva York, Nueva York: WH Freeman.
Reynolds, O. 1883. "Una Investigación Experimental de las circunstancias que determinan si el movimiento del agua será directa o sinuoso, y de la Ley de la Resistencia en canales paralelos." Philosophical Transactions de la Royal Society de Londres 174: 935-82 .
Richardson, LF 1920. "El suministro de energía desde y hacia remolinos atmosféricos." Proceedings of the Royal Society de Londres, serie A , 97 (686): 354-37.
Sloss, LL 1963. "Secuencias en la cratónica interior de América del Norte." Sociedad Geológica de América Boletín 74 (2): 93-113.
Staniforth, A. y J. Côté. 1991. "Esquemas de Integración semi-de Lagrange para los modelos atmosféricos-A Review."Monthly Weather Review 119: 2206-223.
Stokes, G. 1851. "sobre el efecto de la fricción interna de los fluidos en el movimiento de los péndulos." Transacciones de la Sociedad Filosófica de Cambridge 9: 8-106.
Whipple, KX, GS Hancock, y RS Anderson. 2000. "Río incisión en la roca: Mecánica y eficacia relativa de desplume, a la abrasión y cavitación." Geological Society of America Bulletin 112 (1-2): 490-503.
Williamson, DL, JB Drake, JJ Hack, R. Jakob, y PN Swaztrauber. 1992. "Una prueba estándar establecido para numéricas Aproximaciones a las ecuaciones de aguas someras en Geometría esférica." Journal of Computational Physics 102 (1): 211-24.
Winston, D., y PK Enlace, 1993. "Rocas de Medio proterozoicas de Montana, Idaho y Washington: El Cinturón supergrupo." En Precámbrico de la Estados Unidos contiguos . Editado por J. Reed, P. Simms, R. Houston, D. Rankin, P. Link, R. Van Schmus, y P. Bickford, 487-521. Boulder, Colorado: v. Geological Society of America, la geología de América del Norte, C-3.
Wohl, EE 1992. "Bancos roca de fondo y Bares: Boulder. Las inundaciones en el Burdekin Garganta de Australia"Geological Society of America Bulletin 104 (6): 770-78.
Apéndice A: ¿Cuál es la turbulencia del fluido?
La importancia del papel de la turbulencia en los fluidos que se reconoció claramente en la primera parte del siglo 19, cuando la caída de presión en las tuberías de agua y el arrastre de agua en barcos eran problemas hidráulicos de gran interés práctico. Se sabía que tanto la caída de presión en las tuberías y la fricción ejercida sobre los buques mientras se movían a través del agua tenían dos componentes, uno lineal y la otra aproximadamente cuadrática en la velocidad del fluido. Sorprendentemente, se encontró que sólo el primero depende de la viscosidad del fluido. En la década de 1850 G. y H. Hagen Darcy ambos publicados cuidadosas mediciones de flujo de fluido a través de tuberías de gran tamaño. Ambos señalaron que la componente de segundo grado se asoció con el movimiento desordenado en el fluido y que se convirtió en la contribución dominante cuando los tubos eran grandes y la velocidad de flujo se hicieron suficientemente alta. Se especula que el aumento de la resistencia se debe a la energía gastada en la creación de fluctuaciones de la velocidad que el flujo se convirtió en turbulento.
G. Stokes (1851) fue el primero en mostrar que la aparición de flujo turbulento depende de la relación de la fuerza de inercia del fluido en movimiento a las fuerzas viscosas que actúan sobre él. Esta relación se conoce hoy como el número de Reynolds, el nombre de O. Reynolds, que en los años 1870 y 1880 publicó una serie de artículos que describen los resultados de sus estudios experimentales cuidadosos en la transición de laminar a turbulento flujo de fluido, por primera vez en las tuberías y luego en otros ajustes. Reynolds, en un documento de 1883 (Reynolds 1883), hizo hincapié en la importancia de esta relación sin dimensiones que ahora lleva su nombre. Esta relación, el número de Reynolds Re , se expresa por lo general como Re = uL / ν , donde u es la velocidad del fluido, L es una dimensión espacial característica de la corriente, y ν es la viscosidad cinemática.
A principios del siglo 20 Ludwig Prandtl hizo un importante avance computacional mediante la introducción del concepto de una capa límite de fluido. En un artículo de 1905 innovador demostró que las ecuaciones para el flujo de fluido podrían simplificarse dividiendo el campo de flujo en dos regiones: una capa límite en la que la viscosidad del fluido juega un papel importante y la región fuera de la capa límite, en donde la viscosidad puede ser descuidado, sin efectos significativos sobre la solución. La teoría de la capa límite de Prandtl proporciona una nueva comprensión fundamental de arrastre de fricción de la piel y cómo racionalización reduce la resistencia de las alas del avión y otros cuerpos que se mueven con relación a un entorno fluido.
Pero, ¿qué es la turbulencia del fluido? El científico británico LF Richardson (1920) describe la turbulencia del fluido en forma poética de la siguiente manera:
foto de Richardson de turbulencia es un flujo compuesto por una jerarquía de vórtices, o remolinos, de grande a pequeño. Estos remolinos, incluidas las grandes, son inestables. La cizalla que su rotación ejerce sobre el fluido que rodea genera más pequeñas nuevas remolinos. La energía cinética de los remolinos grandes se pasa así a los remolinos más pequeños que surgen de ellos. Estos remolinos más pequeños a su vez se someten a un mismo proceso, dando lugar a remolinos aún más pequeñas que heredan la energía de sus predecesores, y así sucesivamente. De esta manera, la energía se transmite de las grandes escalas de movimiento a escalas más y más pequeños hasta alcanzar una escala de longitud suficientemente pequeño que la viscosidad molecular del fluido transforma la energía cinética de estos remolinos más pequeños en calor.
En 1941, la AN Kolmogorov rusa (1991a, b) postuló que para números de Reynolds muy altos, los movimientos turbulentos pequeña escala son estadísticamente isotrópica (es decir, no tienen dirección espacial preferencial). En general, las mayores escalas de un flujo no son isotrópicas, dado que son determinados por las características geométricas particulares del problema. Idea de Kolmogorov fue que, en la cascada de energía que Richardson describe, esta información geométrica y direccional a la mayor escala se pierde. Esto significa que las estadísticas de las escalas más pequeño tiene un carácter universal y que son los mismos para todos los flujos turbulentos cuando el número de Reynolds es suficientemente alta. Se planteó la hipótesis, además, que para los números de Reynolds muy altas las estadísticas de escalas pequeñas se determinan universalmente y de forma única por la viscosidad ν y la tasa de disipación de energía ε . Con sólo estos dos parámetros, un λ longitud única se puede obtener por análisis dimensional dada por λ = ( v 3 / ε) ¼ . Esto se conoce hoy como la escala de longitud de Kolmogorov.
El concepto de Kolmogorov fue que el flujo turbulento se caracteriza por una jerarquía de escalas través de los cuales la cascada de energía se lleva a cabo. La disipación de la energía cinética se produce a escalas del orden de Kolmogorov longitud λ , mientras que la entrada de energía en la cascada proviene de la descomposición de las grandes escalas, que se caracteriza por la longitud de escala L . Estas dos escalas en los extremos de la cascada pueden variar en varios órdenes de magnitud en altos números de Reynolds. En el medio hay una variedad de escalas (cada una con su propia longitud característica r ) que se ha formado a expensas de la energía de las grandes. Estas escalas son muy grandes en comparación con la longitud de Kolmogorov, pero sigue siendo muy pequeña en comparación con la gran escala del flujo (es decir, λ << r << L ). Desde remolinos de esta gama son mucho más grandes que los remolinos disipativas que existen en las escalas de Kolmogorov, casi toda la energía cinética se disipa en este rango. Más bien, es simplemente transferido a escalas más pequeñas hasta que los efectos viscosos comienzan a llegar a ser importante como la escala de Kolmogorov se aborda. Dentro de este rango de efectos inerciales de las parcelas de fluidos en movimiento son todavía mucho más grande que los efectos viscosos. Por lo tanto dentro de este rango de inercia es posible descuidar los efectos de la viscosidad molecular en la dinámica interna. Aunque algunos detalles adicionales han surgido en los 75 años desde que Kolmogorov publicó estas ideas, la comprensión moderna de la turbulencia recae directamente sobre la imagen básica que proporciona.
La importancia del papel de la turbulencia en los fluidos que se reconoció claramente en la primera parte del siglo 19, cuando la caída de presión en las tuberías de agua y el arrastre de agua en barcos eran problemas hidráulicos de gran interés práctico. Se sabía que tanto la caída de presión en las tuberías y la fricción ejercida sobre los buques mientras se movían a través del agua tenían dos componentes, uno lineal y la otra aproximadamente cuadrática en la velocidad del fluido. Sorprendentemente, se encontró que sólo el primero depende de la viscosidad del fluido. En la década de 1850 G. y H. Hagen Darcy ambos publicados cuidadosas mediciones de flujo de fluido a través de tuberías de gran tamaño. Ambos señalaron que la componente de segundo grado se asoció con el movimiento desordenado en el fluido y que se convirtió en la contribución dominante cuando los tubos eran grandes y la velocidad de flujo se hicieron suficientemente alta. Se especula que el aumento de la resistencia se debe a la energía gastada en la creación de fluctuaciones de la velocidad que el flujo se convirtió en turbulento.
G. Stokes (1851) fue el primero en mostrar que la aparición de flujo turbulento depende de la relación de la fuerza de inercia del fluido en movimiento a las fuerzas viscosas que actúan sobre él. Esta relación se conoce hoy como el número de Reynolds, el nombre de O. Reynolds, que en los años 1870 y 1880 publicó una serie de artículos que describen los resultados de sus estudios experimentales cuidadosos en la transición de laminar a turbulento flujo de fluido, por primera vez en las tuberías y luego en otros ajustes. Reynolds, en un documento de 1883 (Reynolds 1883), hizo hincapié en la importancia de esta relación sin dimensiones que ahora lleva su nombre. Esta relación, el número de Reynolds Re , se expresa por lo general como Re = uL / ν , donde u es la velocidad del fluido, L es una dimensión espacial característica de la corriente, y ν es la viscosidad cinemática.
A principios del siglo 20 Ludwig Prandtl hizo un importante avance computacional mediante la introducción del concepto de una capa límite de fluido. En un artículo de 1905 innovador demostró que las ecuaciones para el flujo de fluido podrían simplificarse dividiendo el campo de flujo en dos regiones: una capa límite en la que la viscosidad del fluido juega un papel importante y la región fuera de la capa límite, en donde la viscosidad puede ser descuidado, sin efectos significativos sobre la solución. La teoría de la capa límite de Prandtl proporciona una nueva comprensión fundamental de arrastre de fricción de la piel y cómo racionalización reduce la resistencia de las alas del avión y otros cuerpos que se mueven con relación a un entorno fluido.
Pero, ¿qué es la turbulencia del fluido? El científico británico LF Richardson (1920) describe la turbulencia del fluido en forma poética de la siguiente manera:
foto de Richardson de turbulencia es un flujo compuesto por una jerarquía de vórtices, o remolinos, de grande a pequeño. Estos remolinos, incluidas las grandes, son inestables. La cizalla que su rotación ejerce sobre el fluido que rodea genera más pequeñas nuevas remolinos. La energía cinética de los remolinos grandes se pasa así a los remolinos más pequeños que surgen de ellos. Estos remolinos más pequeños a su vez se someten a un mismo proceso, dando lugar a remolinos aún más pequeñas que heredan la energía de sus predecesores, y así sucesivamente. De esta manera, la energía se transmite de las grandes escalas de movimiento a escalas más y más pequeños hasta alcanzar una escala de longitud suficientemente pequeño que la viscosidad molecular del fluido transforma la energía cinética de estos remolinos más pequeños en calor.
En 1941, la AN Kolmogorov rusa (1991a, b) postuló que para números de Reynolds muy altos, los movimientos turbulentos pequeña escala son estadísticamente isotrópica (es decir, no tienen dirección espacial preferencial). En general, las mayores escalas de un flujo no son isotrópicas, dado que son determinados por las características geométricas particulares del problema. Idea de Kolmogorov fue que, en la cascada de energía que Richardson describe, esta información geométrica y direccional a la mayor escala se pierde. Esto significa que las estadísticas de las escalas más pequeño tiene un carácter universal y que son los mismos para todos los flujos turbulentos cuando el número de Reynolds es suficientemente alta. Se planteó la hipótesis, además, que para los números de Reynolds muy altas las estadísticas de escalas pequeñas se determinan universalmente y de forma única por la viscosidad ν y la tasa de disipación de energía ε . Con sólo estos dos parámetros, un λ longitud única se puede obtener por análisis dimensional dada por λ = ( v 3 / ε) ¼ . Esto se conoce hoy como la escala de longitud de Kolmogorov.
El concepto de Kolmogorov fue que el flujo turbulento se caracteriza por una jerarquía de escalas través de los cuales la cascada de energía se lleva a cabo. La disipación de la energía cinética se produce a escalas del orden de Kolmogorov longitud λ , mientras que la entrada de energía en la cascada proviene de la descomposición de las grandes escalas, que se caracteriza por la longitud de escala L . Estas dos escalas en los extremos de la cascada pueden variar en varios órdenes de magnitud en altos números de Reynolds. En el medio hay una variedad de escalas (cada una con su propia longitud característica r ) que se ha formado a expensas de la energía de las grandes. Estas escalas son muy grandes en comparación con la longitud de Kolmogorov, pero sigue siendo muy pequeña en comparación con la gran escala del flujo (es decir, λ << r << L ). Desde remolinos de esta gama son mucho más grandes que los remolinos disipativas que existen en las escalas de Kolmogorov, casi toda la energía cinética se disipa en este rango. Más bien, es simplemente transferido a escalas más pequeñas hasta que los efectos viscosos comienzan a llegar a ser importante como la escala de Kolmogorov se aborda. Dentro de este rango de efectos inerciales de las parcelas de fluidos en movimiento son todavía mucho más grande que los efectos viscosos. Por lo tanto dentro de este rango de inercia es posible descuidar los efectos de la viscosidad molecular en la dinámica interna. Aunque algunos detalles adicionales han surgido en los 75 años desde que Kolmogorov publicó estas ideas, la comprensión moderna de la turbulencia recae directamente sobre la imagen básica que proporciona.
Apéndice B: Capas límite turbulento
En este trabajo, la preocupación se centra en la erosión a gran escala y el transporte de sedimentos y procesos de deposición sobre una superficie continental impulsada por una capa de agua turbulenta que se mueve rápidamente.Este problema se encuentra en la categoría general de flujo de canal abierto, que es uno de gran interés práctico y uno que se ha estudiado experimentalmente por muchos años. Ejemplos de flujos de canal abierto incluyen los ríos, las corrientes de marea, canales de riego, y láminas de agua corriendo a través de la superficie del suelo después de una lluvia. Las ecuaciones usadas comúnmente para modelar estas corrientes están anclados en las mediciones experimentales y décadas de validación en muchas aplicaciones diversas. Estos experimentos muestran que, excepto en la proximidad inmediata de la frontera, el perfil de la velocidad media en el régimen de flujo turbulento es muy cerca de ser una función logarítmica de la distancia desde el límite . Si, además, el límite es rugosa debido a la presencia de, por ejemplo, partículas de arena de tamaño discretos que forman el contorno, la velocidad media de ¾ (es decir, la velocidad total con las fluctuaciones de alta frecuencia debido a la turbulencia resta de distancia) como una función de altura z por encima del límite se da a buena aproximación por
donde u τ es lo que se conoce comúnmente como la velocidad de cizallamiento o velocidad de fricción y z o es un número proporcional al tamaño de los elementos de rugosidad a lo largo de la frontera. Este resultado y la breve descripción de la teoría de la capa límite turbulenta que sigue se basan en apuntes para un curso graduado 2009 titulado "Turbulent Boundary Capas" por David Apsley (2009) en la Universidad de Manchester, Reino Unido. Apsley, a su vez, depende en cierta medida de Papa (2000).
La cantidad u τ , que se define como u τ = ( τ o / ρ) ½ , donde τ o es el esfuerzo cortante límite y ρ es la densidad del fluido, de manera consciente debe entenderse como una medida de la tensión de corte límite en lugar de una velocidad real , a pesar de que tiene las dimensiones de la velocidad y que comúnmente se conoce como tal. Utilizando la ecuación.(A1) la velocidad de fricción u τ se puede calcular a partir de la profundidad h de la capa turbulenta y la velocidad media en z = h como u τ = u (h) / [ 2,5 ln (h / z O )] . Suponiendo que la rugosidad límite surge de las partículas de sedimento mineral bastante bien ordenados con el área de distribución natural de la habitual forma de las partículas y la redondez, la cantidad z O está dada por D / 30 , donde D es el tamaño de partícula característico. Para los propósitos de este documento, D es elegida para ser de 0,5 mm (0,019 pulgadas), el valor de uso general para distinguir arena gruesa de arena media. El factor de 2,5 es el recíproco del parámetro von Karman, una cantidad determinada experimentalmente, el nombre de Theodore von Kármán, un ingeniero aeronáutico estadounidense húngaro-considerado por muchos como la aerodinámica teórico por excelencia del siglo 20.
Eq.(A1) proporciona una descripción realista, validada experimentalmente de la velocidad horizontal media y la turbulencia asociada desde unos pocos milímetros por encima del límite de la parte superior de la capa que fluye.Tenga en cuenta que la viscosidad cinemática ν no aparece. Esto es porque en la superficie de la fricción en la superficie está dominada por la rugosidad de las partículas de sedimento y la turbulencia esto genera, en lugar de cizallamiento de la propia agua. La representación del flujo turbulento en términos de la ecuación. (A1) le permite a uno para conectar el campo de la velocidad global del agua obtenida mediante la resolución de las ecuaciones de aguas poco profundas en una esfera en rotación (la tierra) con el modelo más localizada de la erosión, el transporte de sedimentos, y la deposición de sedimentos se describe a continuación.
En este trabajo, la preocupación se centra en la erosión a gran escala y el transporte de sedimentos y procesos de deposición sobre una superficie continental impulsada por una capa de agua turbulenta que se mueve rápidamente.Este problema se encuentra en la categoría general de flujo de canal abierto, que es uno de gran interés práctico y uno que se ha estudiado experimentalmente por muchos años. Ejemplos de flujos de canal abierto incluyen los ríos, las corrientes de marea, canales de riego, y láminas de agua corriendo a través de la superficie del suelo después de una lluvia. Las ecuaciones usadas comúnmente para modelar estas corrientes están anclados en las mediciones experimentales y décadas de validación en muchas aplicaciones diversas. Estos experimentos muestran que, excepto en la proximidad inmediata de la frontera, el perfil de la velocidad media en el régimen de flujo turbulento es muy cerca de ser una función logarítmica de la distancia desde el límite . Si, además, el límite es rugosa debido a la presencia de, por ejemplo, partículas de arena de tamaño discretos que forman el contorno, la velocidad media de ¾ (es decir, la velocidad total con las fluctuaciones de alta frecuencia debido a la turbulencia resta de distancia) como una función de altura z por encima del límite se da a buena aproximación por
donde u τ es lo que se conoce comúnmente como la velocidad de cizallamiento o velocidad de fricción y z o es un número proporcional al tamaño de los elementos de rugosidad a lo largo de la frontera. Este resultado y la breve descripción de la teoría de la capa límite turbulenta que sigue se basan en apuntes para un curso graduado 2009 titulado "Turbulent Boundary Capas" por David Apsley (2009) en la Universidad de Manchester, Reino Unido. Apsley, a su vez, depende en cierta medida de Papa (2000).
La cantidad u τ , que se define como u τ = ( τ o / ρ) ½ , donde τ o es el esfuerzo cortante límite y ρ es la densidad del fluido, de manera consciente debe entenderse como una medida de la tensión de corte límite en lugar de una velocidad real , a pesar de que tiene las dimensiones de la velocidad y que comúnmente se conoce como tal. Utilizando la ecuación.(A1) la velocidad de fricción u τ se puede calcular a partir de la profundidad h de la capa turbulenta y la velocidad media en z = h como u τ = u (h) / [ 2,5 ln (h / z O )] . Suponiendo que la rugosidad límite surge de las partículas de sedimento mineral bastante bien ordenados con el área de distribución natural de la habitual forma de las partículas y la redondez, la cantidad z O está dada por D / 30 , donde D es el tamaño de partícula característico. Para los propósitos de este documento, D es elegida para ser de 0,5 mm (0,019 pulgadas), el valor de uso general para distinguir arena gruesa de arena media. El factor de 2,5 es el recíproco del parámetro von Karman, una cantidad determinada experimentalmente, el nombre de Theodore von Kármán, un ingeniero aeronáutico estadounidense húngaro-considerado por muchos como la aerodinámica teórico por excelencia del siglo 20.
Eq.(A1) proporciona una descripción realista, validada experimentalmente de la velocidad horizontal media y la turbulencia asociada desde unos pocos milímetros por encima del límite de la parte superior de la capa que fluye.Tenga en cuenta que la viscosidad cinemática ν no aparece. Esto es porque en la superficie de la fricción en la superficie está dominada por la rugosidad de las partículas de sedimento y la turbulencia esto genera, en lugar de cizallamiento de la propia agua. La representación del flujo turbulento en términos de la ecuación. (A1) le permite a uno para conectar el campo de la velocidad global del agua obtenida mediante la resolución de las ecuaciones de aguas poco profundas en una esfera en rotación (la tierra) con el modelo más localizada de la erosión, el transporte de sedimentos, y la deposición de sedimentos se describe a continuación.
Apéndice C: transporte de sedimentos en una capa turbulenta de Límites
El siguiente tratamiento de sedimentos en suspensión sigue de cerca la proporcionada por Harris (2003) en sus notas de clase para un curso de posgrado en los procesos de transporte de sedimentos. Suspensión de partículas de sedimento se produce cuando la fluctuación de velocidad turbulenta w ' en la dirección vertical es al menos tan grande como la velocidad de sedimentación w de las partículas. Los experimentos muestran que la velocidad de fluctuación vertical de w ' debido a la turbulencia es aproximadamente igual a la velocidad de fricción u τ , es decir, w' ≈ u τ cerca de la parte inferior de la capa turbulenta. Una cantidad conocida como el parámetro P Rouse, que implica la relación de wa u tau y se define como P = w / κ u τ = 2,5 W / u τ , se usa comúnmente como un criterio para la suspensión. ( Κ es el parámetro de von Karman, cuyo valor es 0,4.) En base a la observación experimental se ha encontrado que para P > 2,5 no hay suspensión, para 1 < P <2,5 no es la suspensión incipiente, y para P <1 hay plena suspensión. Tenga en cuenta que la velocidad de sedimentación de partículas w , y por lo tanto también el parámetro Rouse P , depende del tamaño de partícula.
Para caracterizar la carga de sedimentos de la capa turbulenta de agua, es útil el uso de la fracción de volumen local cde sedimentos en el flujo. Si el flujo es razonablemente uniforme en la dirección horizontal en escalas espaciales en el orden del espesor de la capa, que supondremos, y es razonablemente estable en escalas de tiempo del orden de nuestro paso de tiempo numérica, luego de conservación de la masa se puede demostrar que
donde prima ( ') denota la componente fluctuante y <> denota la media hora. El término < c 'w' > representa difusión vertical de sedimentos en suspensión por remolinos turbulentos. Este término puede ser reescrita en términos de una difusividad Eddy K s como < c 'w' > = K s ∂c / ∂z , y la Ec. (A2), entonces se puede reescribir como
La integración de esta ecuación con respecto a z rendimientos
Esto indica que para las condiciones de régimen uniforme, el asentamiento de sedimentos hacia abajo (- wc ) equilibra la difusión ascendente de sedimentos por los remolinos turbulentos. La integración de una vez más con respecto a la altura usando y como la variable de los rendimientos de integración
donde una es una altura de referencia cerca de la cama donde la concentración de c (a) puede ser especificado. En el flujo turbulento cerca de la cama del eddy viscosidad K m para el impulso viene dada por K m = κ u τ z, donde κ es el parámetro de von Karman, u τ es la velocidad de fricción, y z es la altura. Desde los mismos remolinos que se difunden impulso verticalmente también masa difusa, se puede representar la eddy difusividad K s como K s = ak u τ z, donde α es una constante de proporcionalidad. Para concentraciones bajas de sedimentos α≈ 1, y por altas concentraciones se utiliza comúnmente un valor de 1,35. Sustituyendo esta expresión para K s en el lado derecho de la ecuación. (A5) encontramos
Combinando las ecuaciones. (A5) y (A6) y utilizando el hecho de que el parámetro Rouse P = W / K u τ , se obtiene la siguiente expresión para la fracción de volumen c de sedimentos como una función de la altura z por encima de la cama
Este resultado es válido solamente cerca de la base de la capa turbulenta. Para obtener una descripción que es aplicable en toda la capa turbulenta, es necesario utilizar una difusividad eddy que disminuye más fuertemente con la altura. Una forma funcional de este tipo de uso común se obtiene un perfil de difusividad de Foucault que es parabólica, disminuyendo a cero en la parte superior de la capa turbulenta en z = h y se aproxime ak u τ z cerca de la base de la capa. Se expresa como K s = α κu τ z (1- z / h ). La sustitución de este difusividad eddy cuadrática en la Ec. (A7) se obtiene lo que se conoce como el perfil de Rouse,
Dado que el parámetro Rouse depende de la velocidad de sedimentación de las partículas que a su vez depende del tamaño de partícula, dividimos el sedimento en un número finito de clases de sedimento de acuerdo con el tamaño de partícula que designamos por el subíndice i . Eq. (A8) a continuación, proporciona una distribución vertical separada de la fracción de volumen para cada clase de sedimentos.
La integración de la ecuación. (A8) con respecto a la altura de una a h , señalando que
obtenemos la siguiente expresión para la capacidad de carga F i del flujo para cada clase de sedimentos
Elegimos la altura de referencia de un ser constante con un valor de 1 cm (0,39 pulgadas). Desde c i (a) , la fracción de volumen de sedimento a la altura de una , es adimensional, observamos que F i , tiene unidades de distancia. F irepresenta el espesor total de los sedimentos de la clase i de que el flujo puede suspender. Para los fines del cálculo, ya que, como se explica más adelante, que impone un límite severo sobre la fracción de volumen de sedimento en cada altura, tomamos c i (a) igual a la unidad. Tenga en cuenta que F i entonces sólo depende del parámetro Rouse P i , de la clase de sedimentos y la profundidad de la capa turbulenta h . Por razones prácticas, dividimos la coordenada de la altura z en un número de zonas o capas discretas, indexados por k , y calcular una capacidad de carga de sedimentos F ik para cada capa. La columna total capacidad de carga F i viene dado por F i = Σ F i k , donde la suma es sobre k . En los casos ilustrativos que describimos más adelante, se utiliza un total de siete capas verticales de espesor fijo para representar el perfil de sedimentos en el flujo turbulento.
agua turbulenta puede mantener sólo una fracción del volumen limitado de sedimentos en suspensión. Basado en el trabajo de Bagnold (1966), la fracción de volumen limitando a cualquier altura dada en el flujo, sobre todas las clases de sedimentos, es aproximadamente 0,09. Imponemos este límite en cada una de las capas verticales en cada punto de la rejilla lateral en la malla computacional.
El siguiente tratamiento de sedimentos en suspensión sigue de cerca la proporcionada por Harris (2003) en sus notas de clase para un curso de posgrado en los procesos de transporte de sedimentos. Suspensión de partículas de sedimento se produce cuando la fluctuación de velocidad turbulenta w ' en la dirección vertical es al menos tan grande como la velocidad de sedimentación w de las partículas. Los experimentos muestran que la velocidad de fluctuación vertical de w ' debido a la turbulencia es aproximadamente igual a la velocidad de fricción u τ , es decir, w' ≈ u τ cerca de la parte inferior de la capa turbulenta. Una cantidad conocida como el parámetro P Rouse, que implica la relación de wa u tau y se define como P = w / κ u τ = 2,5 W / u τ , se usa comúnmente como un criterio para la suspensión. ( Κ es el parámetro de von Karman, cuyo valor es 0,4.) En base a la observación experimental se ha encontrado que para P > 2,5 no hay suspensión, para 1 < P <2,5 no es la suspensión incipiente, y para P <1 hay plena suspensión. Tenga en cuenta que la velocidad de sedimentación de partículas w , y por lo tanto también el parámetro Rouse P , depende del tamaño de partícula.
Para caracterizar la carga de sedimentos de la capa turbulenta de agua, es útil el uso de la fracción de volumen local cde sedimentos en el flujo. Si el flujo es razonablemente uniforme en la dirección horizontal en escalas espaciales en el orden del espesor de la capa, que supondremos, y es razonablemente estable en escalas de tiempo del orden de nuestro paso de tiempo numérica, luego de conservación de la masa se puede demostrar que
donde prima ( ') denota la componente fluctuante y <> denota la media hora. El término < c 'w' > representa difusión vertical de sedimentos en suspensión por remolinos turbulentos. Este término puede ser reescrita en términos de una difusividad Eddy K s como < c 'w' > = K s ∂c / ∂z , y la Ec. (A2), entonces se puede reescribir como
La integración de esta ecuación con respecto a z rendimientos
Esto indica que para las condiciones de régimen uniforme, el asentamiento de sedimentos hacia abajo (- wc ) equilibra la difusión ascendente de sedimentos por los remolinos turbulentos. La integración de una vez más con respecto a la altura usando y como la variable de los rendimientos de integración
donde una es una altura de referencia cerca de la cama donde la concentración de c (a) puede ser especificado. En el flujo turbulento cerca de la cama del eddy viscosidad K m para el impulso viene dada por K m = κ u τ z, donde κ es el parámetro de von Karman, u τ es la velocidad de fricción, y z es la altura. Desde los mismos remolinos que se difunden impulso verticalmente también masa difusa, se puede representar la eddy difusividad K s como K s = ak u τ z, donde α es una constante de proporcionalidad. Para concentraciones bajas de sedimentos α≈ 1, y por altas concentraciones se utiliza comúnmente un valor de 1,35. Sustituyendo esta expresión para K s en el lado derecho de la ecuación. (A5) encontramos
Combinando las ecuaciones. (A5) y (A6) y utilizando el hecho de que el parámetro Rouse P = W / K u τ , se obtiene la siguiente expresión para la fracción de volumen c de sedimentos como una función de la altura z por encima de la cama
Este resultado es válido solamente cerca de la base de la capa turbulenta. Para obtener una descripción que es aplicable en toda la capa turbulenta, es necesario utilizar una difusividad eddy que disminuye más fuertemente con la altura. Una forma funcional de este tipo de uso común se obtiene un perfil de difusividad de Foucault que es parabólica, disminuyendo a cero en la parte superior de la capa turbulenta en z = h y se aproxime ak u τ z cerca de la base de la capa. Se expresa como K s = α κu τ z (1- z / h ). La sustitución de este difusividad eddy cuadrática en la Ec. (A7) se obtiene lo que se conoce como el perfil de Rouse,
Dado que el parámetro Rouse depende de la velocidad de sedimentación de las partículas que a su vez depende del tamaño de partícula, dividimos el sedimento en un número finito de clases de sedimento de acuerdo con el tamaño de partícula que designamos por el subíndice i . Eq. (A8) a continuación, proporciona una distribución vertical separada de la fracción de volumen para cada clase de sedimentos.
La integración de la ecuación. (A8) con respecto a la altura de una a h , señalando que
obtenemos la siguiente expresión para la capacidad de carga F i del flujo para cada clase de sedimentos
Elegimos la altura de referencia de un ser constante con un valor de 1 cm (0,39 pulgadas). Desde c i (a) , la fracción de volumen de sedimento a la altura de una , es adimensional, observamos que F i , tiene unidades de distancia. F irepresenta el espesor total de los sedimentos de la clase i de que el flujo puede suspender. Para los fines del cálculo, ya que, como se explica más adelante, que impone un límite severo sobre la fracción de volumen de sedimento en cada altura, tomamos c i (a) igual a la unidad. Tenga en cuenta que F i entonces sólo depende del parámetro Rouse P i , de la clase de sedimentos y la profundidad de la capa turbulenta h . Por razones prácticas, dividimos la coordenada de la altura z en un número de zonas o capas discretas, indexados por k , y calcular una capacidad de carga de sedimentos F ik para cada capa. La columna total capacidad de carga F i viene dado por F i = Σ F i k , donde la suma es sobre k . En los casos ilustrativos que describimos más adelante, se utiliza un total de siete capas verticales de espesor fijo para representar el perfil de sedimentos en el flujo turbulento.
agua turbulenta puede mantener sólo una fracción del volumen limitado de sedimentos en suspensión. Basado en el trabajo de Bagnold (1966), la fracción de volumen limitando a cualquier altura dada en el flujo, sobre todas las clases de sedimentos, es aproximadamente 0,09. Imponemos este límite en cada una de las capas verticales en cada punto de la rejilla lateral en la malla computacional.
D Apéndice: velocidad de sedimentación de las partículas de sedimento
Como hemos visto, la capacidad de un flujo turbulento para suspender las partículas de sedimento y mantenerlas en suspensión depende de la velocidad de sedimentación w de las partículas. El parámetro Rouse P que se produce como el exponente en la fórmula de distribución de sedimentos vertical (A8) implica la relación de la velocidad de sedimentación w a la velocidad de fricción u τ del flujo turbulento. Una gran cantidad de esfuerzo experimental se ha invertido para caracterizar la velocidad de sedimentación de las partículas de sedimento en los últimos 60 años. Para obtener los valores apropiados para w utilizamos una fórmula simple desarrollado por Jiménez y Madsen (2003) que proporciona un buen ajuste a las mediciones experimentales para tamaños de grano entre 0,063 mm (0,0025 in) y 1 mm (0,039 in), cubriendo el intervalo de muy fino a grueso arena. Esta fórmula es
con Y = [(s - 1) gd] ½ y S = 0,25 D y / ν , donde d es el diámetro de grano nominal, s es el peso específico de los granos de sedimento, g es la aceleración gravitacional, ν es la viscosidad cinemática agua, y a y B son constantes derivadas del ajuste a los datos. Asumimos un peso específico s para la arena de 2,65, el valor de g de 9,8 m / s, y una viscosidad cinemática ν para el agua de 10 -6 m 2 / s. Los valores de las constantes A y B previstos por Jiménez y Madsen (2003) son A = 0,954 y B = 5,12. Para cada clase de sedimentos i con el diámetro medio de grano nominal d i aplicamos (A10) para obtener la velocidad de sedimentación w i para esa clase de sedimentos. Para el caso que se describe en este documento elegimos tres clases de sedimentos con diámetros de grano nominales d i de 0,063 mm (0,0025 pulgadas), 0,25 mm (0,010 pulgadas), y 1 mm (0,039 pulgadas), lo que corresponde a la arena fina, arena media, y arena gruesa respectivamente. Arcilla y limo se supone para flocular para formar partículas que muestran sedimentación comportamiento idéntico al de arena fina.
Como hemos visto, la capacidad de un flujo turbulento para suspender las partículas de sedimento y mantenerlas en suspensión depende de la velocidad de sedimentación w de las partículas. El parámetro Rouse P que se produce como el exponente en la fórmula de distribución de sedimentos vertical (A8) implica la relación de la velocidad de sedimentación w a la velocidad de fricción u τ del flujo turbulento. Una gran cantidad de esfuerzo experimental se ha invertido para caracterizar la velocidad de sedimentación de las partículas de sedimento en los últimos 60 años. Para obtener los valores apropiados para w utilizamos una fórmula simple desarrollado por Jiménez y Madsen (2003) que proporciona un buen ajuste a las mediciones experimentales para tamaños de grano entre 0,063 mm (0,0025 in) y 1 mm (0,039 in), cubriendo el intervalo de muy fino a grueso arena. Esta fórmula es
con Y = [(s - 1) gd] ½ y S = 0,25 D y / ν , donde d es el diámetro de grano nominal, s es el peso específico de los granos de sedimento, g es la aceleración gravitacional, ν es la viscosidad cinemática agua, y a y B son constantes derivadas del ajuste a los datos. Asumimos un peso específico s para la arena de 2,65, el valor de g de 9,8 m / s, y una viscosidad cinemática ν para el agua de 10 -6 m 2 / s. Los valores de las constantes A y B previstos por Jiménez y Madsen (2003) son A = 0,954 y B = 5,12. Para cada clase de sedimentos i con el diámetro medio de grano nominal d i aplicamos (A10) para obtener la velocidad de sedimentación w i para esa clase de sedimentos. Para el caso que se describe en este documento elegimos tres clases de sedimentos con diámetros de grano nominales d i de 0,063 mm (0,0025 pulgadas), 0,25 mm (0,010 pulgadas), y 1 mm (0,039 pulgadas), lo que corresponde a la arena fina, arena media, y arena gruesa respectivamente. Arcilla y limo se supone para flocular para formar partículas que muestran sedimentación comportamiento idéntico al de arena fina.
Apéndice E: La erosión y deposición
En la actualidad el modelo de erosión es muy simple. Dado que nuestro interés es la captura de los aspectos más sobresalientes del cataclismo inundación global en el que la velocidad del agua alcanzan varias decenas de metros por segundo, descuidamos los procesos de erosión a velocidades bajas del agua y en lugar de centrarnos en la erosión por cavitación impulsada por el cual se produce a velocidades más altas de agua y resultados en las tasas de erosión extremas. La cavitación implica la formación de vapor de agua y las burbujas de aire que se produce cuando la presión local del fluido cae por debajo de la presión de vapor del aire disuelto (Arndt 1981). daños por cavitación se produce cuando estas burbujas se realizan en regiones de presión más alta y implosionan en las proximidades de la interfaz agua-roca. Los picos de presión generados por la implosión y colapso de estas burbujas son típicamente del orden de varios cientos de MPa, o varios miles de atmósferas (Momber 2003). Tales impulsos de presión exceden la resistencia al corte de la mayoría de minerales de silicato. Por lo tanto, dañan y erosionan las celosías de cristales individuales que componen una roca policristalino (Momber 2003).
Whipple, Hancock, y Anderson (2000) proporcionan la siguiente expresión simple para describir la tasa ë c de la degradación de la superficie en m / s de erosión por cavitación
donde E es una constante de proporcionalidad, u es la velocidad de flujo justo encima de la cama (que se supone en la altura z = a ), y u cav es una velocidad umbral de cavitación. Adoptamos esta relación simple para representar la cavitación en nuestro modelo.
¿Qué valores de q , u CAV , y E podría ser apropiado para la representación de las condiciones extremas que se espera para un cataclismo en la escala de la inundación del Génesis? Los valores para el exponente determinado experimentalmente q tan grande como 7 han sido reportados (Murai et al. 1997). Falvey (1990) asume un valor de qde 6. Varios autores poner q en el rango de 5-7. Elegimos un valor de q de 6. Tenga en cuenta que con q igual a 6, duplicando la diferencia entre T y T CAV aumenta la tasa de erosión por cavitación en un factor de 64. La velocidad umbral de cavitación u cav depende de la profundidad de flujo, el sedimento fino la concentración, el contenido de aire disuelto, y el número de Reynolds. Chanson (1997) observa que en los aliviaderos y desagües de fondo del canal inclinado, daños por cavitación puede comenzar a producirse a velocidades de aguas claras de entre 12 a 15 m / s.Falvey (1990) sugiere que la cavitación puede empezar a ocurrir en aliviaderos a velocidades tan bajas como 10 m / s.En nuestro tratamiento de cavitación se elige un valor de u cav de 15 m / s.
El factor multiplicativo E en la ecuación. (A11) no está tan bien limitados por los datos experimentales. Falvey (1990, 34) menciona un experimento en el que un 13 mm (0,5 pulgadas) del agujero se produjo en concreto durante un período de 3 horas por una de 30 m / s jet, pero casi no se proporcionan detalles del experimento. Estas cifras sugieren una tasa de erosión por cavitación de 1,2 × 10 -6 m / s. Más recientemente Momber (2003) informa de un trabajo experimental para medir las tasas relativas de erosión por cavitación de varios tipos de rocas y hormigón utilizando una cámara de cavitación. Detalles cruciales del experimento no se incluyen en el documento. Sin embargo, las tasas de erosión previstas en mg / s y la zona de los daños causados por las fotografías en el documento implican tasas de erosión del granito y la riolita del orden de 4 x 10 -5 m / s. A la luz de las mediciones disponibles en la actualidad, vemos el valor que hemos elegido (1 x 10 -5 m / s para una velocidad de agua de 20 m / s) como razonable.El descubrimiento de que la cavitación se puede aplicar de manera útil a la roca de perforación está impulsando a los estudios de laboratorio relacionados con estas aplicaciones (por ejemplo, Momber 2003). Esto sugiere que los datos experimentales más para el régimen de cavitación de las velocidades extremadamente altas de agua puede ser pronto próxima.
También se ha propuesto que la cavitación puede operar en conjunción con la abrasión por partículas de sedimento en suspensión para dar las tasas de erosión mucho mayores que por cualquiera de los procesos solo. En el intento de dar cuenta de los muchos ejemplos de campo de la erosión del lecho de rocas masivas, toscamente articulados, especialmente características de estrías y la espeleología, Whipple, Hancock, y Anderson (2000), en el contexto de la erosión de la abrasión por la carga de sedimentos en suspensión, observación :
Con la frase, "saltating vigorosamente partículas," se están refiriendo a rebotar partículas de carga de fondo en lugar de partículas suspendidas en el flujo turbulento. Ya han argumentado que la tasa de erosión de la abrasión de sedimentos en suspensión, además de la mejora de cavitación, debe escalar con la quinta potencia de la velocidad justo por encima de la cama (Whipple, Hancock, y Anderson de 2000, la Ec. 10), y por lo tanto que posiblemente puede ser comparable a la velocidad de erosión que dan para la erosión por cavitación. Los dos procesos que actúan en conjunto sin duda deben involucrar a tasas mucho más altas que actúan solos. Sin embargo, en nuestro modelo incluimos solamente erosión por cavitación y elegir un valor de u cav de 15 m / s, un valor de q , de 6, y un valor de E de 0,00001 / (20-15) 6 = 6,4 × 10 -10 , lo que implica una tasa de erosión de 10 -5 m / s o 10 micrómetros / s para una velocidad de flujo en de 20 m / s a la altura z = una . Creemos que esto es muy conservador para el intervalo de velocidad en la que se produce la cavitación.
El tratamiento de deposición es sencillo. Los sedimentos en suspensión en la capa inferior que es en exceso de la capacidad de carga de esa capa se declara que es la deposición. En cada punto de la cuadrícula se añade el sedimento recién depositada, por clase, a una matriz de la deposición de sedimentos y también se retira de la matriz de suspensión de sedimentos para la capa vertical de más inferior. Esta prueba se realiza en el proceso paso a paso de tiempo después de que las nuevas alturas de columna de agua de nivel de tiempo y velocidades han sido calculada, tras los perfiles de sedimentos en suspensión han sido actualizados para tener en cuenta el transporte de agua, y después de la nueva sedimentos capacidades de carga se han calculado. Si el flujo turbulento no ha alcanzado su capacidad de suspender los sedimentos y si el flujo es suficientemente rápida para erosionar la base, que permita la erosión y la suspensión de las partículas erosionadas resultantes.
Para nuestra aplicación, nos cuenta la posible presencia de una alta concentración de sedimentos en la proximidad de la superficie. Hacemos esto mediante la ampliación de E por el factor (1 - 10 C ), donde C = Σc i (a) es la suma sobre todas las clases de sedimentos de sus fracciones en volumen dentro del intervalo de 0,01-1 m de altura (capa 1), con este suma restringido por el tratamiento de sedimentación sea no mayor que 0,1. Esta restricción implica que cuando la fracción de volumen total de sedimentos dentro de la capa más inferior alcanza 0,1, la erosión cesa. Además, limitamos E tal que no exceda del 20% de la columna residual capacidad de carga, es decir, 0,2 veces la diferencia entre la columna de capacidad de carga y la carga total de sedimentos. Por simplicidad, usamos estos valores de parámetros, independientemente de la profundidad de flujo y el número de Reynolds. Cuando el material de lecho es roca de fondo cristalino de sedimentos y no, se utilizan los mismos parámetros excepto que aumentamos E por un factor de tres para tener en cuenta la suavidad relativa del sedimento. Una prueba se hace para asegurarse de que toda la cubierta de sedimentos existente se erosiona antes de que ocurra cualquier erosión lecho de roca.
Asumimos además que la cavitación degrada lecho de roca granítica cristalina en una distribución de tamaños de partículas que corresponden a 70% de arena fina, 20% de arena de medio, y 10% de arena gruesa. Esta elección está motivada principalmente por nuestra evaluación de la distribución que es característica del registro sedimentario de la tierra. Implícito en este asume la distribución de tamaños de partículas es el supuesto adicional de que las partículas de arcilla y de limos flocular y se comportan como arena fina en su comportamiento de sedimentación. Además, para los propósitos de este estudio exploratorio, ignoramos los sedimentos carbonatados. También observamos que los experimentos que proporcionan una distribución de tamaño de partícula fiable de la cavitación que actúa sobre rocas de silicatos cristalinos son en su mayoría carecen en este punto en el tiempo.
Después de que el cálculo de la erosión se ha realizado, se añade el sedimento recién erosionado al perfil de sedimento en suspensión dividiendo el espesor del sedimento erosionado, para cada clase de sedimentos, por la altura de la columna de agua y multiplicando por espesor de la capa para la contribución a cada capa. Dado que es posible en una capa dada por la concentración de sedimentos que exceda la capacidad de carga, que frente a esta situación. Después de que el nuevo tiempo alturas de columna de agua de nivel y las velocidades han sido calculada, tras los perfiles de sedimentos en suspensión han sido actualizados para tener en cuenta el transporte de agua, y después de la nueva sedimentos capacidades de carga se han calculado, pero antes de que el cálculo de la erosión se ha realizado, nos permitir el asentamiento de sedimentos en la capa de abajo. La cantidad transferida es igual al paso de tiempo (en segundos) multiplicado por la velocidad de sedimentación (en metros por segundo) de la clase de sedimentos en particular, pero limitado por el exceso de sedimento en la capa (en metros) relativo a la capacidad de la capa de transporte (en metros ). Comenzamos con el procedimiento de la capa superior.
Las cantidades acumuladas de la erosión y la deposición, así como las cantidades instantáneas de sedimento en suspensión por clase, como una función de la posición sobre la superficie, se realiza un seguimiento como el tiempo de paso a paso avanza.
En la actualidad el modelo de erosión es muy simple. Dado que nuestro interés es la captura de los aspectos más sobresalientes del cataclismo inundación global en el que la velocidad del agua alcanzan varias decenas de metros por segundo, descuidamos los procesos de erosión a velocidades bajas del agua y en lugar de centrarnos en la erosión por cavitación impulsada por el cual se produce a velocidades más altas de agua y resultados en las tasas de erosión extremas. La cavitación implica la formación de vapor de agua y las burbujas de aire que se produce cuando la presión local del fluido cae por debajo de la presión de vapor del aire disuelto (Arndt 1981). daños por cavitación se produce cuando estas burbujas se realizan en regiones de presión más alta y implosionan en las proximidades de la interfaz agua-roca. Los picos de presión generados por la implosión y colapso de estas burbujas son típicamente del orden de varios cientos de MPa, o varios miles de atmósferas (Momber 2003). Tales impulsos de presión exceden la resistencia al corte de la mayoría de minerales de silicato. Por lo tanto, dañan y erosionan las celosías de cristales individuales que componen una roca policristalino (Momber 2003).
Whipple, Hancock, y Anderson (2000) proporcionan la siguiente expresión simple para describir la tasa ë c de la degradación de la superficie en m / s de erosión por cavitación
donde E es una constante de proporcionalidad, u es la velocidad de flujo justo encima de la cama (que se supone en la altura z = a ), y u cav es una velocidad umbral de cavitación. Adoptamos esta relación simple para representar la cavitación en nuestro modelo.
¿Qué valores de q , u CAV , y E podría ser apropiado para la representación de las condiciones extremas que se espera para un cataclismo en la escala de la inundación del Génesis? Los valores para el exponente determinado experimentalmente q tan grande como 7 han sido reportados (Murai et al. 1997). Falvey (1990) asume un valor de qde 6. Varios autores poner q en el rango de 5-7. Elegimos un valor de q de 6. Tenga en cuenta que con q igual a 6, duplicando la diferencia entre T y T CAV aumenta la tasa de erosión por cavitación en un factor de 64. La velocidad umbral de cavitación u cav depende de la profundidad de flujo, el sedimento fino la concentración, el contenido de aire disuelto, y el número de Reynolds. Chanson (1997) observa que en los aliviaderos y desagües de fondo del canal inclinado, daños por cavitación puede comenzar a producirse a velocidades de aguas claras de entre 12 a 15 m / s.Falvey (1990) sugiere que la cavitación puede empezar a ocurrir en aliviaderos a velocidades tan bajas como 10 m / s.En nuestro tratamiento de cavitación se elige un valor de u cav de 15 m / s.
El factor multiplicativo E en la ecuación. (A11) no está tan bien limitados por los datos experimentales. Falvey (1990, 34) menciona un experimento en el que un 13 mm (0,5 pulgadas) del agujero se produjo en concreto durante un período de 3 horas por una de 30 m / s jet, pero casi no se proporcionan detalles del experimento. Estas cifras sugieren una tasa de erosión por cavitación de 1,2 × 10 -6 m / s. Más recientemente Momber (2003) informa de un trabajo experimental para medir las tasas relativas de erosión por cavitación de varios tipos de rocas y hormigón utilizando una cámara de cavitación. Detalles cruciales del experimento no se incluyen en el documento. Sin embargo, las tasas de erosión previstas en mg / s y la zona de los daños causados por las fotografías en el documento implican tasas de erosión del granito y la riolita del orden de 4 x 10 -5 m / s. A la luz de las mediciones disponibles en la actualidad, vemos el valor que hemos elegido (1 x 10 -5 m / s para una velocidad de agua de 20 m / s) como razonable.El descubrimiento de que la cavitación se puede aplicar de manera útil a la roca de perforación está impulsando a los estudios de laboratorio relacionados con estas aplicaciones (por ejemplo, Momber 2003). Esto sugiere que los datos experimentales más para el régimen de cavitación de las velocidades extremadamente altas de agua puede ser pronto próxima.
También se ha propuesto que la cavitación puede operar en conjunción con la abrasión por partículas de sedimento en suspensión para dar las tasas de erosión mucho mayores que por cualquiera de los procesos solo. En el intento de dar cuenta de los muchos ejemplos de campo de la erosión del lecho de rocas masivas, toscamente articulados, especialmente características de estrías y la espeleología, Whipple, Hancock, y Anderson (2000), en el contexto de la erosión de la abrasión por la carga de sedimentos en suspensión, observación :
Con la frase, "saltating vigorosamente partículas," se están refiriendo a rebotar partículas de carga de fondo en lugar de partículas suspendidas en el flujo turbulento. Ya han argumentado que la tasa de erosión de la abrasión de sedimentos en suspensión, además de la mejora de cavitación, debe escalar con la quinta potencia de la velocidad justo por encima de la cama (Whipple, Hancock, y Anderson de 2000, la Ec. 10), y por lo tanto que posiblemente puede ser comparable a la velocidad de erosión que dan para la erosión por cavitación. Los dos procesos que actúan en conjunto sin duda deben involucrar a tasas mucho más altas que actúan solos. Sin embargo, en nuestro modelo incluimos solamente erosión por cavitación y elegir un valor de u cav de 15 m / s, un valor de q , de 6, y un valor de E de 0,00001 / (20-15) 6 = 6,4 × 10 -10 , lo que implica una tasa de erosión de 10 -5 m / s o 10 micrómetros / s para una velocidad de flujo en de 20 m / s a la altura z = una . Creemos que esto es muy conservador para el intervalo de velocidad en la que se produce la cavitación.
El tratamiento de deposición es sencillo. Los sedimentos en suspensión en la capa inferior que es en exceso de la capacidad de carga de esa capa se declara que es la deposición. En cada punto de la cuadrícula se añade el sedimento recién depositada, por clase, a una matriz de la deposición de sedimentos y también se retira de la matriz de suspensión de sedimentos para la capa vertical de más inferior. Esta prueba se realiza en el proceso paso a paso de tiempo después de que las nuevas alturas de columna de agua de nivel de tiempo y velocidades han sido calculada, tras los perfiles de sedimentos en suspensión han sido actualizados para tener en cuenta el transporte de agua, y después de la nueva sedimentos capacidades de carga se han calculado. Si el flujo turbulento no ha alcanzado su capacidad de suspender los sedimentos y si el flujo es suficientemente rápida para erosionar la base, que permita la erosión y la suspensión de las partículas erosionadas resultantes.
Para nuestra aplicación, nos cuenta la posible presencia de una alta concentración de sedimentos en la proximidad de la superficie. Hacemos esto mediante la ampliación de E por el factor (1 - 10 C ), donde C = Σc i (a) es la suma sobre todas las clases de sedimentos de sus fracciones en volumen dentro del intervalo de 0,01-1 m de altura (capa 1), con este suma restringido por el tratamiento de sedimentación sea no mayor que 0,1. Esta restricción implica que cuando la fracción de volumen total de sedimentos dentro de la capa más inferior alcanza 0,1, la erosión cesa. Además, limitamos E tal que no exceda del 20% de la columna residual capacidad de carga, es decir, 0,2 veces la diferencia entre la columna de capacidad de carga y la carga total de sedimentos. Por simplicidad, usamos estos valores de parámetros, independientemente de la profundidad de flujo y el número de Reynolds. Cuando el material de lecho es roca de fondo cristalino de sedimentos y no, se utilizan los mismos parámetros excepto que aumentamos E por un factor de tres para tener en cuenta la suavidad relativa del sedimento. Una prueba se hace para asegurarse de que toda la cubierta de sedimentos existente se erosiona antes de que ocurra cualquier erosión lecho de roca.
Asumimos además que la cavitación degrada lecho de roca granítica cristalina en una distribución de tamaños de partículas que corresponden a 70% de arena fina, 20% de arena de medio, y 10% de arena gruesa. Esta elección está motivada principalmente por nuestra evaluación de la distribución que es característica del registro sedimentario de la tierra. Implícito en este asume la distribución de tamaños de partículas es el supuesto adicional de que las partículas de arcilla y de limos flocular y se comportan como arena fina en su comportamiento de sedimentación. Además, para los propósitos de este estudio exploratorio, ignoramos los sedimentos carbonatados. También observamos que los experimentos que proporcionan una distribución de tamaño de partícula fiable de la cavitación que actúa sobre rocas de silicatos cristalinos son en su mayoría carecen en este punto en el tiempo.
Después de que el cálculo de la erosión se ha realizado, se añade el sedimento recién erosionado al perfil de sedimento en suspensión dividiendo el espesor del sedimento erosionado, para cada clase de sedimentos, por la altura de la columna de agua y multiplicando por espesor de la capa para la contribución a cada capa. Dado que es posible en una capa dada por la concentración de sedimentos que exceda la capacidad de carga, que frente a esta situación. Después de que el nuevo tiempo alturas de columna de agua de nivel y las velocidades han sido calculada, tras los perfiles de sedimentos en suspensión han sido actualizados para tener en cuenta el transporte de agua, y después de la nueva sedimentos capacidades de carga se han calculado, pero antes de que el cálculo de la erosión se ha realizado, nos permitir el asentamiento de sedimentos en la capa de abajo. La cantidad transferida es igual al paso de tiempo (en segundos) multiplicado por la velocidad de sedimentación (en metros por segundo) de la clase de sedimentos en particular, pero limitado por el exceso de sedimento en la capa (en metros) relativo a la capacidad de la capa de transporte (en metros ). Comenzamos con el procedimiento de la capa superior.
Las cantidades acumuladas de la erosión y la deposición, así como las cantidades instantáneas de sedimento en suspensión por clase, como una función de la posición sobre la superficie, se realiza un seguimiento como el tiempo de paso a paso avanza.
Apéndice F: Efecto de la carga de sedimentos en Topografía
Se encontró temprano en la probar el modelo que el sedimento espesores de varios cientos de metros rutinariamente surgir. Cuando se les permitió tan grandes espesores para aumentar la topografía continente original sin compensación isostática en absoluto, se observó un tipo de inestabilidad numérica. Este comportamiento implicó la formación de montículos localizadas de sedimentos, por lo general unos pocos cientos de kilómetros de diámetro y cientos de metros de altura. Esta topografía, a su vez, obligó al flujo de agua a concentrarse en los canales entre estos montículos de sedimento y para mejorar la deposición que se produzca en la parte superior de los montículos en las profundidades y velocidades de flujo eran pequeños. Cuanto mayores sean los montículos crecieron, más fuerte esta tendencia se hizo. Un remedio simple para este problema es incluir algún grado de compensación isostática para permitir el sótano a disminuir en respuesta a la carga de sedimentos por encima de ella. El régimen de compensación elegido proporciona una compensación del 10% para las cargas menos de 400 m (1.312 pies), aumentando a una compensación del 30% para una carga de 1200 m (3936 pies) y una compensación del 50% para una carga de 2000 m (6561 pies). Para la parte de la carga en exceso de 2000 m (6561 pies), se aplica la compensación de 90%.compensación simétrica se implementa para las cargas negativas producidas por el material eliminado por la erosión del lecho de roca. Ciertamente, esta receta es sólo uno de los muchos que podrían haber sido elegidos. Sus principales características son que la compensación es instantánea, que la fracción de los aumentos de compensación monótonamente al aumentar la altura de la carga de sedimentos, y que existe una compensación casi completa para cargas superiores a 2000 m (6561 pies) de espesor. La suposición de que la compensación es instantánea sería, en principio, parece difícil de justificar, ni de manera aproximada. Sin embargo, si se tiene en cuenta la reducción extrema de resistencia de la roca a lo largo del manto causado por el mecanismo de debilitamiento estrés asociado con placas litosféricas fugitivos y plumas del manto, se hace más plausible. Los cálculos muestran que el debilitamiento, que comienza en la proximidad de una losa o penacho que está entrando en el régimen fuera de control, se propaga rápidamente para abarcar todo el manto. La reducción de la resistencia de la roca a lo largo de la capa a continuación, se aproxima a un factor de un mil millones. Esta reducción en la resistencia de la roca también afecta a la litosfera.Implica una respuesta rápida de la litosfera continental a la carga de la superficie durante la inundación, mientras que el manto se encuentra en su estado debilitado.
Se encontró Dicha compensación casi instantánea para suprimir el comportamiento inesperado de una manera eficaz.Sin embargo, el comportamiento puede ser así no computacional sino que en realidad puede ser reflejo de la realidad física. Como tal, está claro que merece más estudio. Esto es especialmente cierto dado que la tendencia del flujo para formar montículos de producción de sedimentos más vigorosa localizada de flujo de agua, más intensa erosión, y en última instancia mayores volúmenes de sedimentos. Sin embargo, como una exploración más profunda será diferido hasta más tarde y se considera más allá del alcance de la presente comunicación.
Se encontró temprano en la probar el modelo que el sedimento espesores de varios cientos de metros rutinariamente surgir. Cuando se les permitió tan grandes espesores para aumentar la topografía continente original sin compensación isostática en absoluto, se observó un tipo de inestabilidad numérica. Este comportamiento implicó la formación de montículos localizadas de sedimentos, por lo general unos pocos cientos de kilómetros de diámetro y cientos de metros de altura. Esta topografía, a su vez, obligó al flujo de agua a concentrarse en los canales entre estos montículos de sedimento y para mejorar la deposición que se produzca en la parte superior de los montículos en las profundidades y velocidades de flujo eran pequeños. Cuanto mayores sean los montículos crecieron, más fuerte esta tendencia se hizo. Un remedio simple para este problema es incluir algún grado de compensación isostática para permitir el sótano a disminuir en respuesta a la carga de sedimentos por encima de ella. El régimen de compensación elegido proporciona una compensación del 10% para las cargas menos de 400 m (1.312 pies), aumentando a una compensación del 30% para una carga de 1200 m (3936 pies) y una compensación del 50% para una carga de 2000 m (6561 pies). Para la parte de la carga en exceso de 2000 m (6561 pies), se aplica la compensación de 90%.compensación simétrica se implementa para las cargas negativas producidas por el material eliminado por la erosión del lecho de roca. Ciertamente, esta receta es sólo uno de los muchos que podrían haber sido elegidos. Sus principales características son que la compensación es instantánea, que la fracción de los aumentos de compensación monótonamente al aumentar la altura de la carga de sedimentos, y que existe una compensación casi completa para cargas superiores a 2000 m (6561 pies) de espesor. La suposición de que la compensación es instantánea sería, en principio, parece difícil de justificar, ni de manera aproximada. Sin embargo, si se tiene en cuenta la reducción extrema de resistencia de la roca a lo largo del manto causado por el mecanismo de debilitamiento estrés asociado con placas litosféricas fugitivos y plumas del manto, se hace más plausible. Los cálculos muestran que el debilitamiento, que comienza en la proximidad de una losa o penacho que está entrando en el régimen fuera de control, se propaga rápidamente para abarcar todo el manto. La reducción de la resistencia de la roca a lo largo de la capa a continuación, se aproxima a un factor de un mil millones. Esta reducción en la resistencia de la roca también afecta a la litosfera.Implica una respuesta rápida de la litosfera continental a la carga de la superficie durante la inundación, mientras que el manto se encuentra en su estado debilitado.
Se encontró Dicha compensación casi instantánea para suprimir el comportamiento inesperado de una manera eficaz.Sin embargo, el comportamiento puede ser así no computacional sino que en realidad puede ser reflejo de la realidad física. Como tal, está claro que merece más estudio. Esto es especialmente cierto dado que la tendencia del flujo para formar montículos de producción de sedimentos más vigorosa localizada de flujo de agua, más intensa erosión, y en última instancia mayores volúmenes de sedimentos. Sin embargo, como una exploración más profunda será diferido hasta más tarde y se considera más allá del alcance de la presente comunicación.
Apéndice G: Resolviendo para el flujo de agua Uso del agua superficial aproximación
Para describir el flujo de agua sobre la tierra utilizamos las denominadas ecuaciones de aguas someras aplicados a una esfera en rotación. Por el agua superficial se entiende que la profundidad del agua está en todas partes pequeñas en comparación con las escalas horizontales de interés. Las cuencas de los océanos de hoy tienen profundidades medias de alrededor de 4 km (2,5 millas), mientras que la red de cómputo de la superficie de la tierra para los casos que describimos en este artículo tiene un espaciado de puntos de rejilla horizontal de aproximadamente 120 km (74,5 millas). Las profundidades del mar prevista sobre las regiones continentales donde nuestros principales mentiras de interés aún son mucho más pequeños que los de las cuencas oceánicas. Por consiguiente, la aproximación aguas poco profundas es uno apropiado para este problema, uno que permite que el flujo de agua sobre la superficie del globo a ser tratado en términos de una sola capa de agua con espesor lateralmente variable. Lo que de otro modo sería un costoso problema tridimensional se convierte ahora en uno de dos dimensiones mucho más manejable.
Las ecuaciones de aguas poco profundas en una esfera giratoria pueden expresarse (Williamson et al., 1992, 213)
y
donde h es la profundidad del agua, u es la velocidad horizontal (en la esfera), f es el parámetro de Coriolis (igual a 2Ω pecado θ para la tasa de rotación Ω y latitud θ), k es el vector unitario radial hacia el exterior, g es la aceleración gravitacional, y h † es la altura de la superficie libre por encima de una cierta superficie de referencia esférica. Aquí se supone que el agua es homogénea en su composición, incompresible, y invicid. Si h t denota la topografía en la esfera, entonces h † = h + h t . El d / dt operador es el material o la velocidad de un tiempo sustancial o co-movimiento de cambio de una parcela individual de fluido. El ∇ operador es el operador gradiente horizontal esférica y el ∇ • operador es el operador divergencia horizontal esférica. Los símbolos en negrita corresponden a las cantidades vectoriales. Eq.(A12) es una expresión de la conservación de la masa, mientras que la ecuación. (A13) es una expresión de la conservación del momento lineal. Como se mencionó anteriormente, esta formulación de dos dimensiones en términos de una sola capa en la dirección radial es apropiada cuando la profundidad del agua es pequeño en comparación con los importantes escalas de longitud horizontales.
En nuestro problema de las profundidades de agua por encima de las regiones continentales son mucho más pequeños en comparación con los de las regiones oceánicas y continentales en estas regiones donde el agua es poco profunda que esperan una fuerte turbulencia. Por lo tanto, la hipótesis de que el flujo es invicid no es el apropiado, y tenemos que tener en cuenta la fuerte fricción que se produce en la superficie de los continentes de agua. Una forma sencilla de hacer esto es añadir un término de fricción inferior en el lado derecho de la ecuación. (A13) de la forma - ßu / (h + 1 ) , donde β es un parámetro de escala con unidades de m / s. Debido a que los términos de la ecuación. (A13) tienen dimensiones de fuerza por unidad de masa, este término arrastre requiere la división por el agua de profundidad h de ser coherente. La adición de 1 a h en el denominador es evitar que el término general se haga excesivamente grande como la profundidad del agua se aproxima a cero. También es común en los modelos oceánicos incluir en la ecuación de momento un término viscosidad turbulenta llamada que busca representar los efectos de la turbulencia en las escalas no resueltas por la red computacional. La dicha formulación más simple es un término proporcional al operador laplaciano 2-D ∇ 2 = ∇ • ∇ sobre la esfera aplica al campo de velocidad, es decir, un término de la forma γ ∇ 2 u , donde γ es un parámetro de escala con unidades m2 / s. Tenga en cuenta que γ depende de la resolución de la cuadrícula. Los valores típicos son 1 × 10 -3 para β y 2 × 10 -11 para γ cuando el espaciado de la malla es de 120 km (74,5 millas). La incorporación de estos dos términos en el lado derecho de la ecuación de movimiento. (A13) los rendimientos
Tenga en cuenta que en las regiones continentales la profundidad del agua puede disminuir a cero. Por lo tanto, una restricción la profundidad del agua h siempre que seamos no negativo y la velocidad del agua u igual a cero cuando hes cero. También se restrinja el lado derecho de la ecuación. (A14) para ser cero cuando h es cero.
Ecs.(A12) y (A14) se resuelven de manera discreta sobre una malla construida a partir del icosaedro regular como se muestra en la Fig. 1. Un sistema esférico de coordenadas se define por separado en cada nodo de tal manera que el ecuador del sistema pasa a través del nodo y los ejes de longitud y latitud locales están alineados con el este global y direcciones norte. Este enfoque tiene la ventaja de que las coordenadas son casi cartesiano y sólo se necesitan dos componentes (tangencial) de velocidad. Una formulación semi-Lagrange (Staniforth y Cote, 1991) de las ecuaciones.(A12) y (A14) se utiliza lo que implica el cálculo de las trayectorias durante el paso de tiempo que termina en cada nodo. Los valores de h y u al comienzo de la etapa de tiempo en el punto de partida de cada trayectoria se encuentran por interpolación de los valores nodales conocidos en el comienzo de la etapa de tiempo. Los cambios en h y U a lo largo de la trayectoria se calculan utilizando las ecuaciones. (A12) y (A14). Este método de Lagrange-como elimina la mayor parte del ruido de difusión numérica que está asociado con los regímenes de Euler. Un esquema de interpolación exacta de segundo orden se utiliza para encontrar los valores de los puntos de partida de las trayectorias. Esta formulación utilizando la malla icosaédrica ha sido cuidadosamente validado utilizando el conjunto de problemas de prueba desarrollados por Williamson et al. (1992). También constituye la base para el modelo de predicción meteorológica mundial conocida como GME desarrolló a finales de 1990 por el Servicio Meteorológico de Alemania en el que ahora es utilizado por más de 20 otras naciones (Majewski et al., 2002).
Para describir el flujo de agua sobre la tierra utilizamos las denominadas ecuaciones de aguas someras aplicados a una esfera en rotación. Por el agua superficial se entiende que la profundidad del agua está en todas partes pequeñas en comparación con las escalas horizontales de interés. Las cuencas de los océanos de hoy tienen profundidades medias de alrededor de 4 km (2,5 millas), mientras que la red de cómputo de la superficie de la tierra para los casos que describimos en este artículo tiene un espaciado de puntos de rejilla horizontal de aproximadamente 120 km (74,5 millas). Las profundidades del mar prevista sobre las regiones continentales donde nuestros principales mentiras de interés aún son mucho más pequeños que los de las cuencas oceánicas. Por consiguiente, la aproximación aguas poco profundas es uno apropiado para este problema, uno que permite que el flujo de agua sobre la superficie del globo a ser tratado en términos de una sola capa de agua con espesor lateralmente variable. Lo que de otro modo sería un costoso problema tridimensional se convierte ahora en uno de dos dimensiones mucho más manejable.
Las ecuaciones de aguas poco profundas en una esfera giratoria pueden expresarse (Williamson et al., 1992, 213)
y
donde h es la profundidad del agua, u es la velocidad horizontal (en la esfera), f es el parámetro de Coriolis (igual a 2Ω pecado θ para la tasa de rotación Ω y latitud θ), k es el vector unitario radial hacia el exterior, g es la aceleración gravitacional, y h † es la altura de la superficie libre por encima de una cierta superficie de referencia esférica. Aquí se supone que el agua es homogénea en su composición, incompresible, y invicid. Si h t denota la topografía en la esfera, entonces h † = h + h t . El d / dt operador es el material o la velocidad de un tiempo sustancial o co-movimiento de cambio de una parcela individual de fluido. El ∇ operador es el operador gradiente horizontal esférica y el ∇ • operador es el operador divergencia horizontal esférica. Los símbolos en negrita corresponden a las cantidades vectoriales. Eq.(A12) es una expresión de la conservación de la masa, mientras que la ecuación. (A13) es una expresión de la conservación del momento lineal. Como se mencionó anteriormente, esta formulación de dos dimensiones en términos de una sola capa en la dirección radial es apropiada cuando la profundidad del agua es pequeño en comparación con los importantes escalas de longitud horizontales.
En nuestro problema de las profundidades de agua por encima de las regiones continentales son mucho más pequeños en comparación con los de las regiones oceánicas y continentales en estas regiones donde el agua es poco profunda que esperan una fuerte turbulencia. Por lo tanto, la hipótesis de que el flujo es invicid no es el apropiado, y tenemos que tener en cuenta la fuerte fricción que se produce en la superficie de los continentes de agua. Una forma sencilla de hacer esto es añadir un término de fricción inferior en el lado derecho de la ecuación. (A13) de la forma - ßu / (h + 1 ) , donde β es un parámetro de escala con unidades de m / s. Debido a que los términos de la ecuación. (A13) tienen dimensiones de fuerza por unidad de masa, este término arrastre requiere la división por el agua de profundidad h de ser coherente. La adición de 1 a h en el denominador es evitar que el término general se haga excesivamente grande como la profundidad del agua se aproxima a cero. También es común en los modelos oceánicos incluir en la ecuación de momento un término viscosidad turbulenta llamada que busca representar los efectos de la turbulencia en las escalas no resueltas por la red computacional. La dicha formulación más simple es un término proporcional al operador laplaciano 2-D ∇ 2 = ∇ • ∇ sobre la esfera aplica al campo de velocidad, es decir, un término de la forma γ ∇ 2 u , donde γ es un parámetro de escala con unidades m2 / s. Tenga en cuenta que γ depende de la resolución de la cuadrícula. Los valores típicos son 1 × 10 -3 para β y 2 × 10 -11 para γ cuando el espaciado de la malla es de 120 km (74,5 millas). La incorporación de estos dos términos en el lado derecho de la ecuación de movimiento. (A13) los rendimientos
Tenga en cuenta que en las regiones continentales la profundidad del agua puede disminuir a cero. Por lo tanto, una restricción la profundidad del agua h siempre que seamos no negativo y la velocidad del agua u igual a cero cuando hes cero. También se restrinja el lado derecho de la ecuación. (A14) para ser cero cuando h es cero.
Ecs.(A12) y (A14) se resuelven de manera discreta sobre una malla construida a partir del icosaedro regular como se muestra en la Fig. 1. Un sistema esférico de coordenadas se define por separado en cada nodo de tal manera que el ecuador del sistema pasa a través del nodo y los ejes de longitud y latitud locales están alineados con el este global y direcciones norte. Este enfoque tiene la ventaja de que las coordenadas son casi cartesiano y sólo se necesitan dos componentes (tangencial) de velocidad. Una formulación semi-Lagrange (Staniforth y Cote, 1991) de las ecuaciones.(A12) y (A14) se utiliza lo que implica el cálculo de las trayectorias durante el paso de tiempo que termina en cada nodo. Los valores de h y u al comienzo de la etapa de tiempo en el punto de partida de cada trayectoria se encuentran por interpolación de los valores nodales conocidos en el comienzo de la etapa de tiempo. Los cambios en h y U a lo largo de la trayectoria se calculan utilizando las ecuaciones. (A12) y (A14). Este método de Lagrange-como elimina la mayor parte del ruido de difusión numérica que está asociado con los regímenes de Euler. Un esquema de interpolación exacta de segundo orden se utiliza para encontrar los valores de los puntos de partida de las trayectorias. Esta formulación utilizando la malla icosaédrica ha sido cuidadosamente validado utilizando el conjunto de problemas de prueba desarrollados por Williamson et al. (1992). También constituye la base para el modelo de predicción meteorológica mundial conocida como GME desarrolló a finales de 1990 por el Servicio Meteorológico de Alemania en el que ahora es utilizado por más de 20 otras naciones (Majewski et al., 2002).



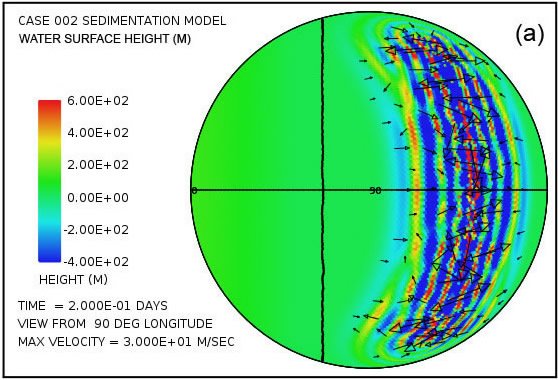
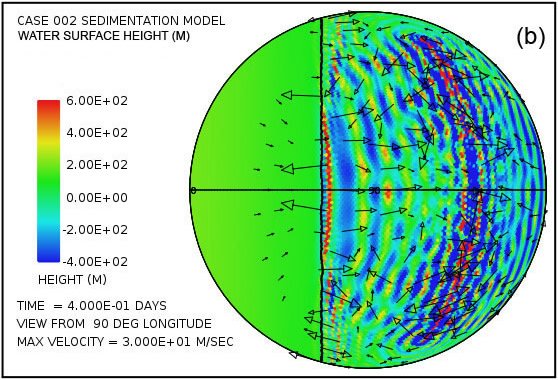

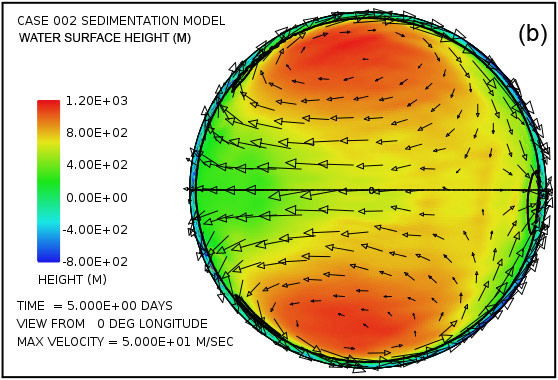

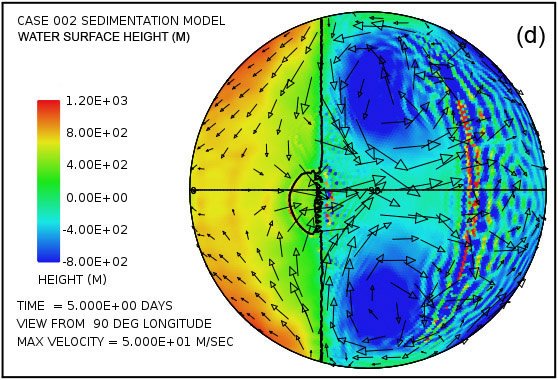
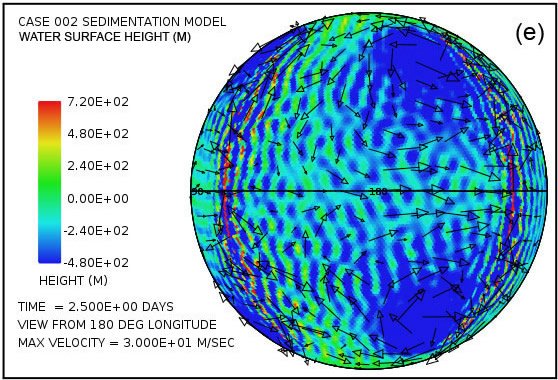
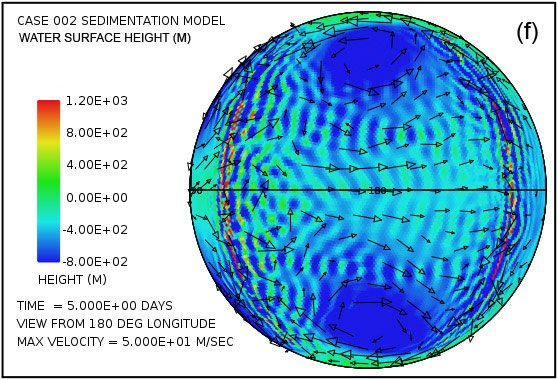
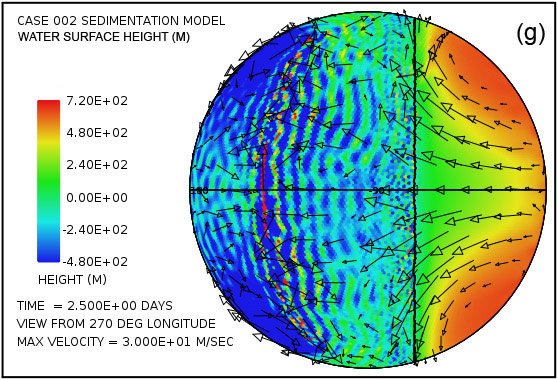


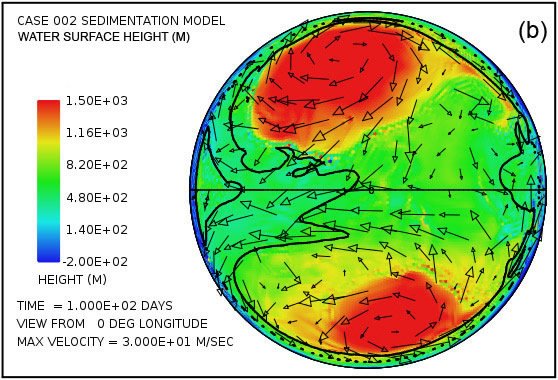
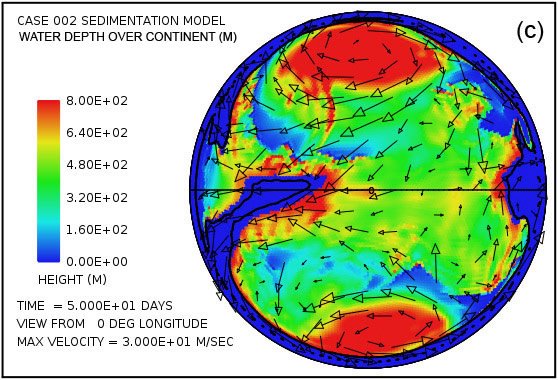
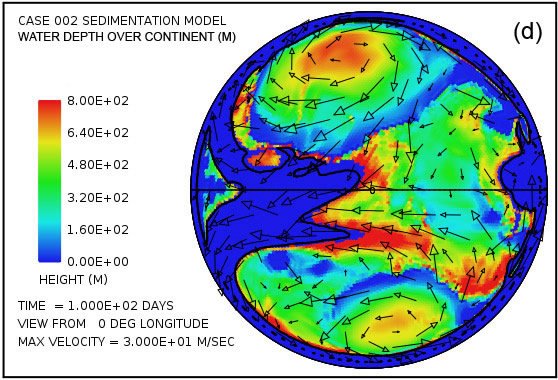
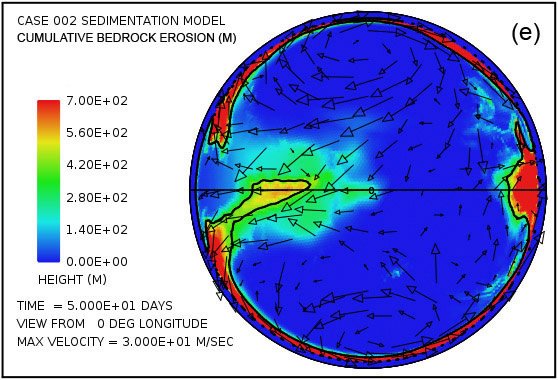
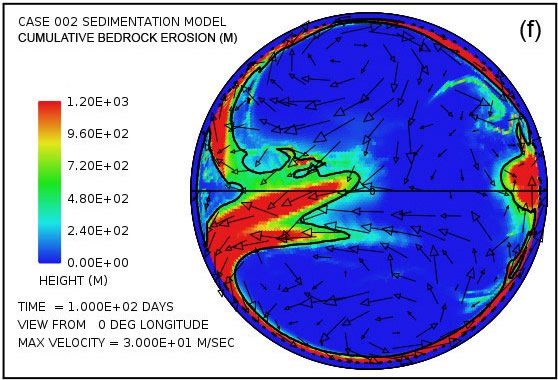
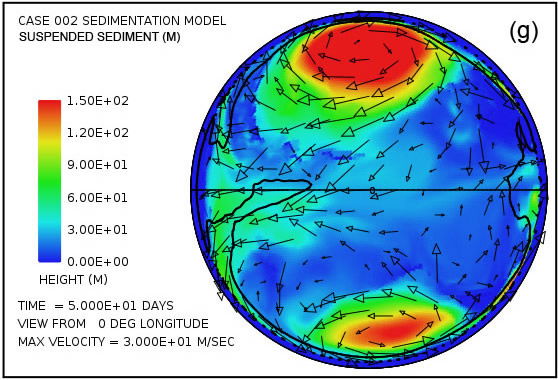
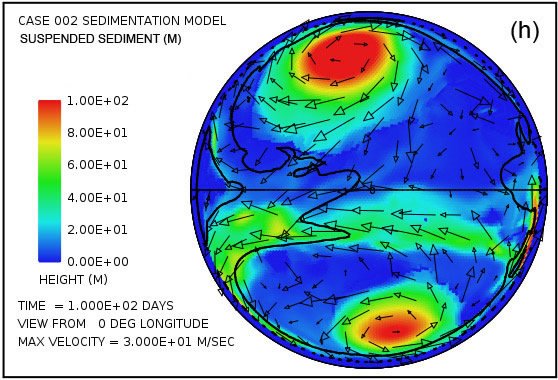
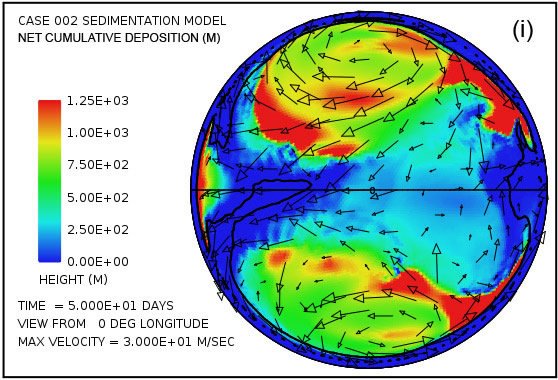
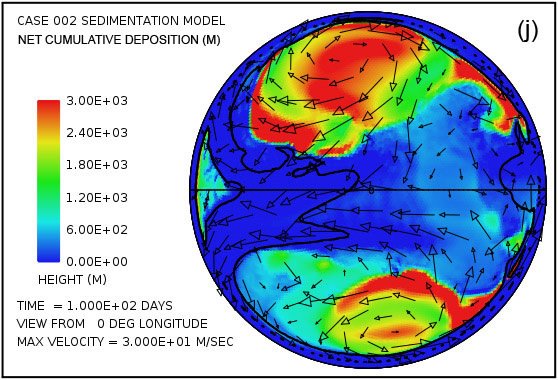

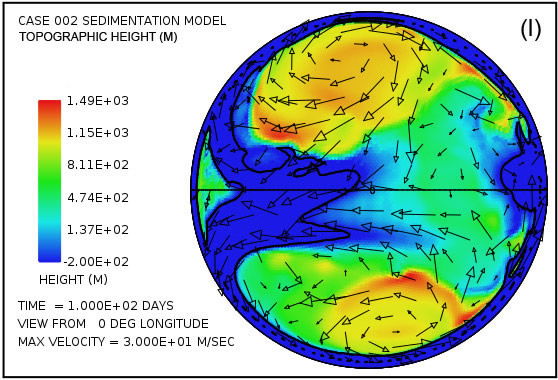
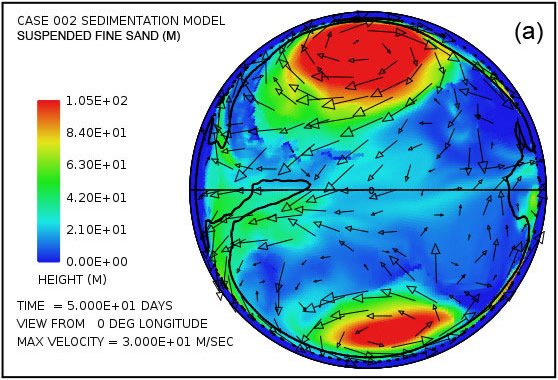
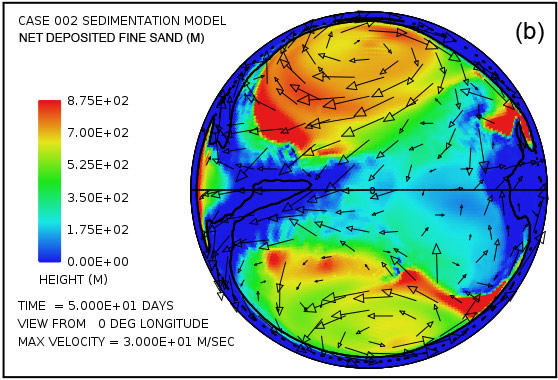
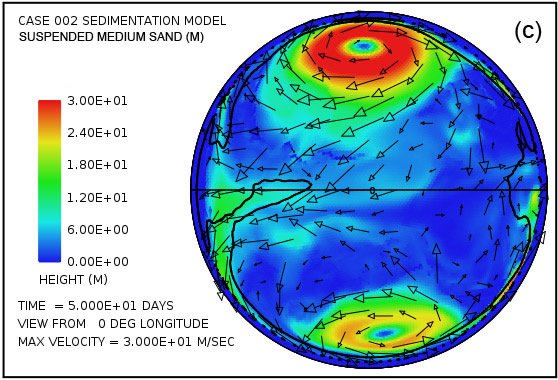
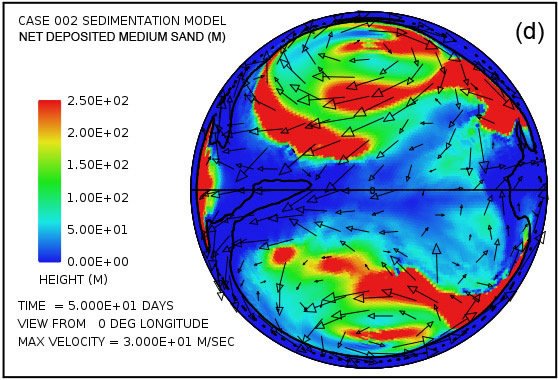
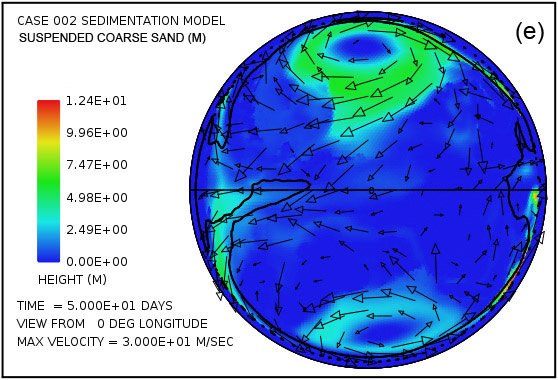
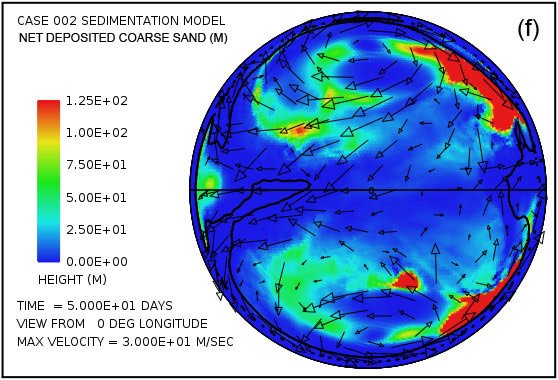
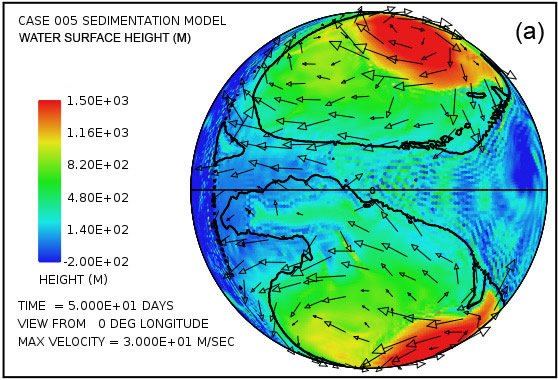
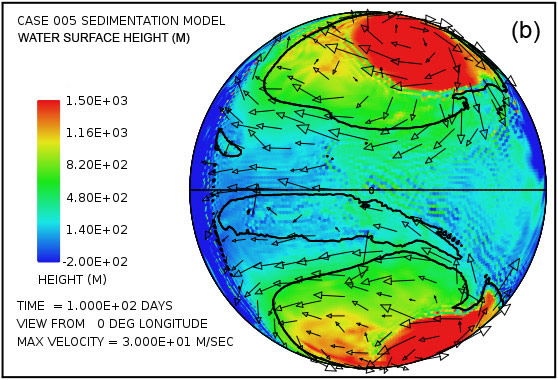
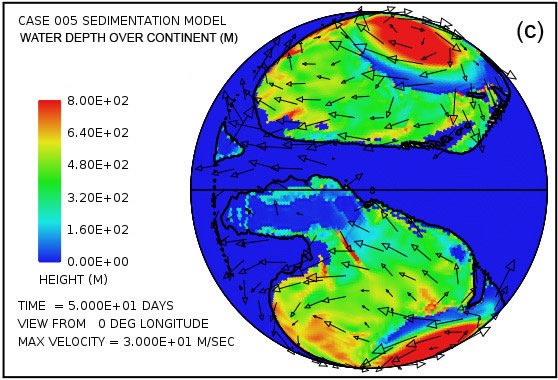
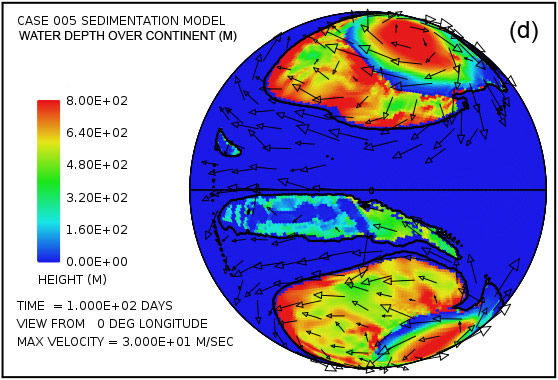
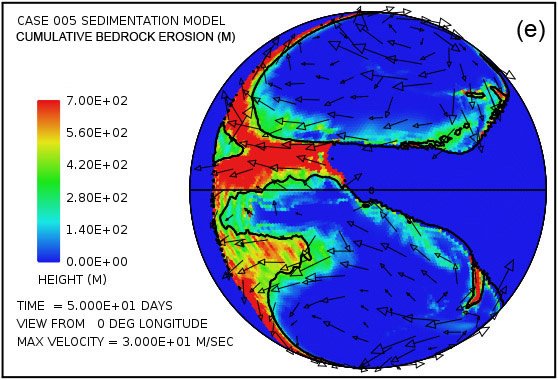
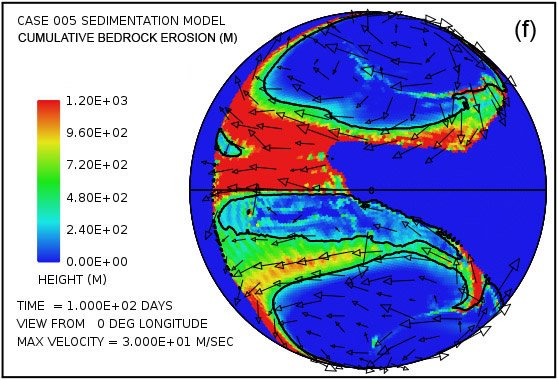

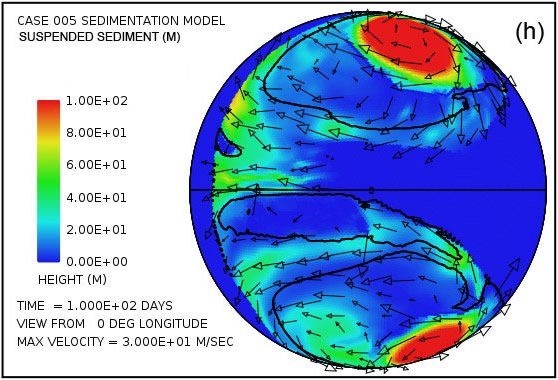
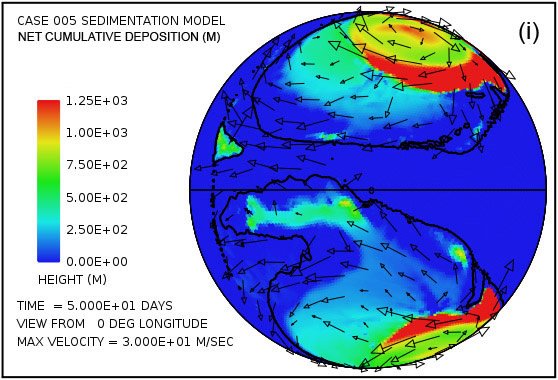

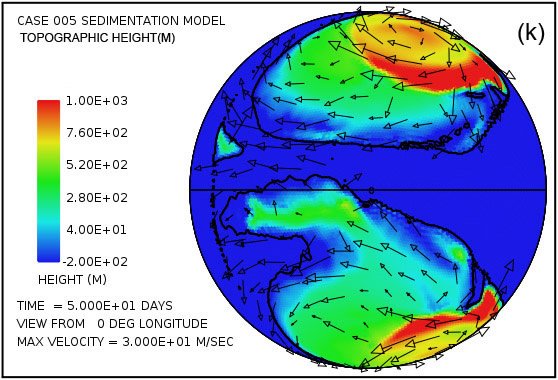
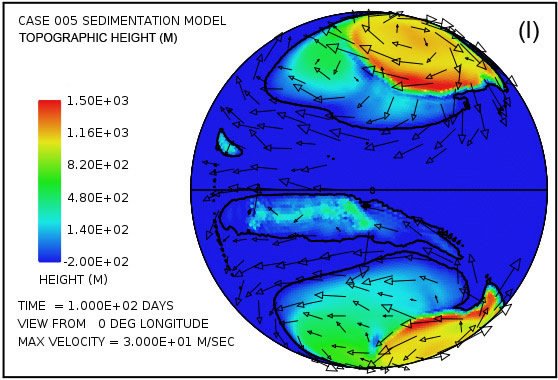
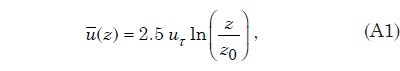
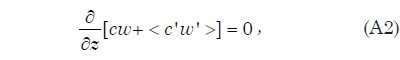
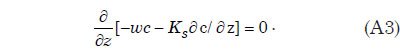
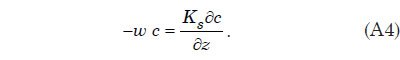
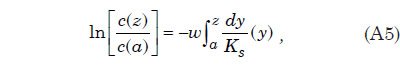
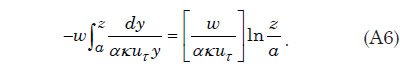
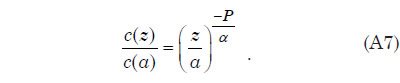
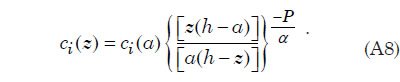
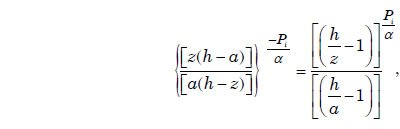
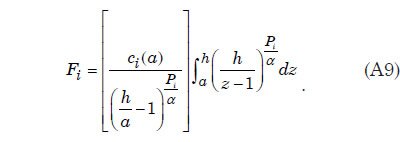
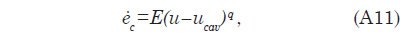
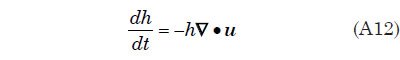
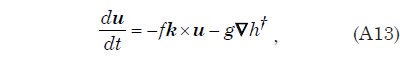
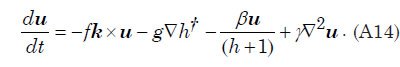
Publicar un comentario